Question

15．在△ABC中，∠BAC=α，邊AB的垂直平分線交邊BC于點D，邊AC的垂直平分線交邊BC于點E，連結AD，AE，則∠DAE的度數為2α-180°或180°-2α．（用含α的代數式表示）

Answer 1

分析 分兩種情況進行討論，先根據線段垂直平分線的性質，得到∠B=∠BAD，∠C=∠CAE，進而得到∠BAD+∠CAE=∠B+∠C=180°-α，再根據角的和差關系進行計算即可．

解答 解：分兩種情況：
①如圖所示，當∠BAC≥90°時，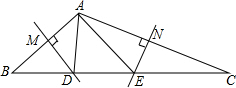

∵DM垂直平分AB，
∴DA=DB，
∴∠B=∠BAD，
同理可得，∠C=∠CAE，
∴∠BAD+∠CAE=∠B+∠C=180°-α，
∴∠DAE=∠BAC-（∠BAD+∠CAE）=α-（180°-α）=2α-180°；
②如圖所示，當∠BAC＜90°時，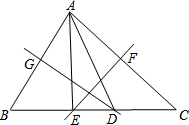

∵DM垂直平分AB，
∴DA=DB，
∴∠B=∠BAD，
同理可得，∠C=∠CAE，
∴∠BAD+∠CAE=∠B+∠C=180°-α，
∴∠DAE=∠BAD+∠CAE-∠BAC=180°-α-α=180°-2α．
故答案為：2α-180°或180°-2α．

點評 本題考查了三角形內角和定理，線段垂直平分線性質的應用，注意：線段垂直平分線上的點到線段兩個端點的距離相等．