
分析 ①利用等量關系:利潤150=每件商品的利潤×賣出的件數=(售價-進價)×賣出的件數,列出方程解答即可;
②利用總利潤=每件商品的利潤×賣出的件數列出函數關系式即可;
③得出自變量的取值范圍,應用二次函數的性質,求最大值即可.
解答 解:(1)設該商品的進價為m元,由題意得40×0.9-m=20%•m,
∴m=30,
答:該商品的進價為30元;
(2)由題意得(x-30)(162-3x)=420,
∴x1=40,x2=44,
答:每件商品的銷售價應定為40元或44元;
(3)在不打折的情況下,商場獲得的利潤為w元,
由題意得:w=(x-30)(162-3x)=-3(x-42)2+432 (30≤x≤54),
∵a=-3<0,
∴當x=42時,w最大=432,
答:如果商場要想獲得最大利潤,每件商品的銷售價定為42元為最合適?最大銷售利潤為432元.
點評 本題考查了二次函數的應用,解題的關鍵是從實際問題中整理出二次函數模型,并運用二次函數的知識解決實際問題.


科目:初中數學 來源: 題型:填空題
 有理數a,b在數軸上的對應位置如圖所示,則下列說法正確的有①④(填序號).
有理數a,b在數軸上的對應位置如圖所示,則下列說法正確的有①④(填序號).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,矩形ABCD中,E是邊BC的一點,F是邊CD的中點,CE=k•BE,且四邊形AECF的面積為2.
如圖,矩形ABCD中,E是邊BC的一點,F是邊CD的中點,CE=k•BE,且四邊形AECF的面積為2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
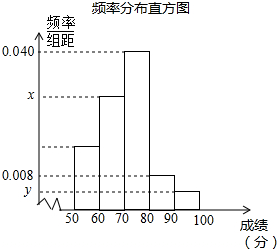 為參加學校的“我愛古詩詞”知識競賽,小王所在班級組織了一次古詩詞知識測試,并將全班同學的分數(得分取正整數,滿分為100分)進行統計,以下是根據這次測試成績制作的不完整的頻率分布表和頻率分布直方圖.
為參加學校的“我愛古詩詞”知識競賽,小王所在班級組織了一次古詩詞知識測試,并將全班同學的分數(得分取正整數,滿分為100分)進行統計,以下是根據這次測試成績制作的不完整的頻率分布表和頻率分布直方圖. | 組別 | 分組 | 頻數 | 頻率 |
| 1 | 50≤x<60 | 9 | 0.18 |
| 2 | 60≤x<70 | a | |
| 3 | 70≤x<80 | 20 | 0.40 |
| 4 | 80≤x<90 | 0.08 | |
| 5 | 90≤x≤100 | 2 | b |
| 合計 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com