Question

16．如圖，將矩形ABCD置于平面直角坐標系中，其中AD邊在x軸上，AB=2，直線MN：y=x-4沿x軸的負方向以每秒1個單位的長度平移，設在平移過程中該直線被矩形ABCD的邊截得的線段長度為m，平移時間為t，m與t的函數圖象如圖2所示．
（1）點A的坐標為（1，0），矩形ABCD的面積為8；
（2）求a，b的值；
（3）在平移過程中，求直線MN掃過矩形ABCD的面積S與t的函數關系式，并寫出自變量t的取值范圍．

Answer 1

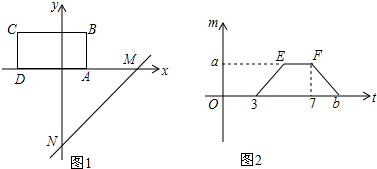
分析 （1）根據直線解析式求出點N的坐標，然后根據函數圖象可知直線平移3個單位后經過點A，從而求的點A的坐標，由點F的橫坐標可求得點D的坐標，從而可求得AD的長，據此可求得ABCD的面積；
（2）如圖1所示；當直線MN經過點B時，直線MN交DA于點E，首先求得點E的坐標，然后利用勾股定理可求得BE的長，從而得到a的值；如圖2所示，當直線MN經過點C時，直線MN交x軸于點F，求得直線MN與x軸交點F的坐標從而可求得b的值；
（3）當0≤t＜3時，直線MN與矩形沒有交點；當3≤t＜5時，如圖3所示S=△EFA的面積；當5≤t＜7時，如圖4所示：S=S_BEFG+S_ABG；當7≤t≤9時，如圖5所示．S=S_ABCD-S_CEF．

解答 解：（1）令直線y=x-4的y=0得：x-4=0，解得：x=4，
∴點M的坐標為（4，0）．
由函數圖象可知：當t=3時，直線MN經過點A，
∴點A的坐標為（1，0）
沿x軸的負方向平移3個單位后與矩形ABCD相交于點A，
∵y=x-4沿x軸的負方向平移3個單位后直線的解析式是：y=x+3-4=x-1，
∴點A的坐標為 （1，0）；
由函數圖象可知：當t=7時，直線MN經過點D，
∴點D的坐標為（-3，0）．
∴AD=4．
∴矩形ABCD的面積=AB•AD=4×2=8．
（2）如圖1所示；當直線MN經過點B時，直線MN交DA于點E．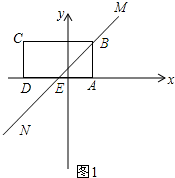

∵點A的坐標為（1，0），
∴點B的坐標為（1，2）
設直線MN的解析式為y=x+c，
將點B的坐標代入得；1+c=2．
∴c=1．
∴直線MN的解析式為y=x+1．
將y=0代入得：x+1=0，解得x=-1，
∴點E的坐標為（-1，0）．
∴BE=$\sqrt{A{E}^{2}+A{B}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$．
∴a=2$\sqrt{2}$
如圖2所示，當直線MN經過點C時，直線MN交x軸于點F．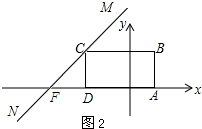

∵點D的坐標為（-3，0），
∴點C的坐標為（-3，2）．
設MN的解析式為y=x+d，將（-3，2）代入得：-3+d=2，解得d=5．
∴直線MN的解析式為y=x+5．
將y=0代入得x+5=0，解得x=-5．
∴點F的坐標為（-5，0）．
∴b=4-（-5）=9．
（3）當0≤t＜3時，直線MN與矩形沒有交點．
∴s=0．
當3≤t＜5時，如圖3所示；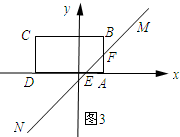

S=${S}_{△AEF}=\frac{1}{2}AE•AF$=$\frac{1}{2}（t-3）^{2}$=$\frac{1}{2}{t}^{2}-3t+\frac{9}{2}$；
當5≤t＜7時，如圖4所示：過點B作BG∥MN．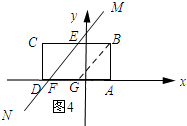

由（2）可知點G的坐標為（-1，0）．
∴FG=t-5．
∴S=S_BEFG+S_ABG=2（t-5）+$\frac{1}{2}×2×2$=2t-8．
當7≤t≤9時，如圖5所示．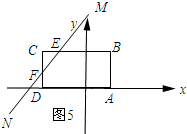

FD=t-7，CF=2-DF=2-（t-7）=9-t．
S=S_ABCD-S_CEF=8-$\frac{1}{2}（9-t）^{2}$=$-\frac{1}{2}{t}^{2}+9t-\frac{65}{2}$．
綜上所述，S與t的函數關系式為S=$\left\{\begin{array}{l}{0（0≤t＜3）}\\{\frac{1}{2}{t}^{2}-3t+\frac{9}{2}（3≤t＜5）}\\{2t-8（5≤t＜7）}\\{-\frac{1}{2}{t}^{2}+9t-\frac{65}{2}（7≤t≤9）}\end{array}\right.$．

點評 本題主要考查的是一次函數的綜合應用，解答本題需要同學們熟練掌握矩形的性質、待定系數法求一次函數的解析式、勾股定理、三角形、平行四邊形、矩形的面積公式，根據題意分類畫出圖形是解題的關鍵．