
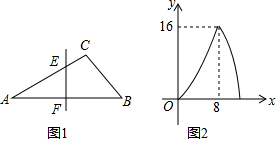
分析 當點E在AC上時,根據已知條件得到EF=$\frac{1}{2}$AF=$\frac{1}{2}$x,根據三角形的面積公式列方程即可得到結論;如圖1,過C作CG⊥AB于G,由如圖2知,當E與C,F與G重合時,△AEF的面積最大,此時,x=8,y=16,求得AG=8,CG=4,得到AB=12,當點E在BC上時,根據三角形的面積公式即可得到結論.
解答 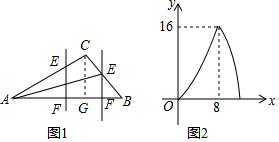 解:當點E在AC上時,
解:當點E在AC上時,
∵EF⊥AB,tan∠A=$\frac{1}{2}$,
∴EF=$\frac{1}{2}$AF=$\frac{1}{2}$x,
∴y=$\frac{1}{2}$×$\frac{1}{2}$x•x=$\frac{1}{4}$x2,
∴y=8時,即$\frac{1}{4}$x2=8,
解得x=4$\sqrt{2}$(負值舍去),
如圖1,過C作CG⊥AB于G,
由如圖2知,當E與C,F與G重合時,
△AEF的面積最大,此時,x=8,y=16,
即AG=8,CG=4,
∵∠B=45°,
∴BG=CG=4,
∴AB=12,
當點E在BC上時,
y=$\frac{1}{2}$•x•(12-x)=-$\frac{1}{2}$x2+6x,
∴y=8時,即-$\frac{1}{2}$x2+6x=8,
解得x=6+2$\sqrt{5}$(負值舍去),
∴當y=8時,x的值是4$\sqrt{2}$或6+2$\sqrt{5}$,
故答案為:4$\sqrt{2}$或6+2$\sqrt{5}$.
點評 本題考查了動點問題的函數圖象,三角形的面積的計算,函數與圖形的性質,掌握的識別圖象是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
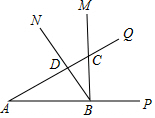 如圖,∠PAQ=∠MBN=30°,∠MBN的頂點B在射線AP上,射線BM和射線BN分別交射線AQ于點C、D,當∠MBN繞點B轉動時.若AB=2$\sqrt{3}$,則CA•CD的最小值是( )
如圖,∠PAQ=∠MBN=30°,∠MBN的頂點B在射線AP上,射線BM和射線BN分別交射線AQ于點C、D,當∠MBN繞點B轉動時.若AB=2$\sqrt{3}$,則CA•CD的最小值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 4 | D. | 12 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,有一張長方形紙板,在它的四角各剪去一個同樣的正方形,然后將四周突出的部分折起,制成一個高為a的長方體形狀的無蓋紙盒.如果紙盒的容積為4a2b,底面長方形的一邊長為b(b<4a),求長方形紙板的面積.
如圖,有一張長方形紙板,在它的四角各剪去一個同樣的正方形,然后將四周突出的部分折起,制成一個高為a的長方體形狀的無蓋紙盒.如果紙盒的容積為4a2b,底面長方形的一邊長為b(b<4a),求長方形紙板的面積.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com