Question

13．如圖1，△ABC中，AG⊥BC于點G，以A為直角頂點，分別以AB、AC為直角邊，向△ABC作等腰Rt△ABE和等腰Rt△ACF，過點E、F作射線GA的垂線，垂足分別為P、Q．
（1）求證：△AEP≌△BAG；
（2）試探究EP與FQ之間的數量關系，并證明你的結論；
（3）如圖2，若連接EF交GA的延長線于H，由（2）中的結論你能判斷EH與FH的大小關系嗎？并說明理由；

Answer 1

分析 （1）根據等腰Rt△ABE的性質，求出∠EPA=∠EAB=∠AGB=90°，∠PEA=∠BAG，根據AAS推出△EPA≌△AGB；
（2）根據全等三角形的性質推出EP=AG，同理可得△FQA≌△AGC，即可得出AG=FQ，最后等量代換即可得出答案；
（3）求出∠EPH=∠FQH=90°，根據AAS推出△EPH≌△FQH，即可得出EH與FH的大小關系；

解答 解：（1）如圖1，∵∠EAB=90°，EP⊥AG，AG⊥BC，
∴∠EPA=∠EAB=∠AGB=90°，
∴∠PEA+∠EAP=90°，∠EAP+∠BAG=90°，
∴∠PEA=∠BAG，
在△EPA和△AGB中，
$\left\{\begin{array}{l}{∠EPA=∠BGA}\\{∠PEA=∠BAG}\\{AE=AB}\end{array}\right.$，
∴△EPA≌△AGB（AAS），

（2）EP=FQ，
證明：由（1）可得，△EPA≌△AGB，
∴EP=AG，
同理可得，△FQA≌△AGC，
∴AG=FQ，
∴EP=FQ；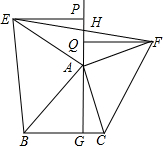

（3）EH=FH，
理由：如圖，∵EP⊥AG，FQ⊥AG，
∴∠EPH=∠FQH=90°，
在△EPH和△FQH中，
$\left\{\begin{array}{l}{∠EHP=∠FHQ}\\{∠EPH=∠FQH}\\{EP=FQ}\end{array}\right.$，
∴△EPH≌△FQH（AAS），
∴EH=FH．

點評 本題屬于三角形綜合題，主要考查了全等三角形的性質和判定以及等腰直角三角形的性質的綜合應用，解題時注意：全等三角形的對應邊相等，對應角相等．等腰直角三角形是一種特殊的三角形，具有所有三角形的性質，還具備等腰三角形和直角三角形的所有性質．