
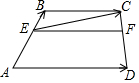
 如圖,在梯形ABCD中,AD∥BC,AD=3,BC=2,點E、F分別在兩腰上,
如圖,在梯形ABCD中,AD∥BC,AD=3,BC=2,點E、F分別在兩腰上,分析 (1)作BM∥CD交AD、EF于M、N兩點,將問題轉化到△ABM中,利用相似三角形的判定與性質求EN,由EF=EN+NF=EN+AD進行求解;
(2)由$\frac{BC}{AD}$=$\frac{2}{3}$、$\frac{EB}{AB}$=$\frac{1}{3}$得BC=$\frac{2}{3}$AD,EB=$\frac{1}{3}$AB,根據$\overrightarrow{EC}$=$\overrightarrow{EB}+\overrightarrow{BC}$可得答案.
解答 解:(1)作BM∥CD交AD、EF于M、N兩點,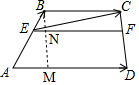
又AD∥BC,EF∥AD,
∴四邊形BCFN與MNFD均為平行四邊形.
∴BC=NF=MD=2,
∴AM=AD-MD=1.
又$\frac{AE}{EB}$=2,
∴$\frac{BE}{BA}$=$\frac{1}{3}$,
∵EF∥AD,
∴△BEN∽△BAM,
∴$\frac{BE}{BA}=\frac{EN}{AM}$,即$\frac{1}{3}=\frac{EN}{1}$,
∴EN=$\frac{1}{3}$,
則EF=EN+NF=$\frac{7}{3}$;
(2)∵$\frac{BC}{AD}$=$\frac{2}{3}$,$\frac{EB}{AB}$=$\frac{1}{3}$,
∴BC=$\frac{2}{3}$AD,EB=$\frac{1}{3}$AB,
∴$\overrightarrow{EB}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{b}$,$\overrightarrow{EB}$=$\frac{1}{3}$$\overrightarrow{AB}$=$\frac{1}{3}$$\overrightarrow{a}$,
則$\overrightarrow{EC}$=$\overrightarrow{EB}+\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$.
點評 本題主要考查了平行四邊形的判定與性質、相似三角形的判定與性質及向量的運算,熟練掌握相似三角形的判定與性質得出對應邊的長度之比和向量的基本運算是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,對稱軸為直線x=-1,與x軸的一個交點為(1,0),與y軸的交點為(0,3),則方程ax2+bx+c=0(a≠0)的解為x1=1,x2=-3.
二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,對稱軸為直線x=-1,與x軸的一個交點為(1,0),與y軸的交點為(0,3),則方程ax2+bx+c=0(a≠0)的解為x1=1,x2=-3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
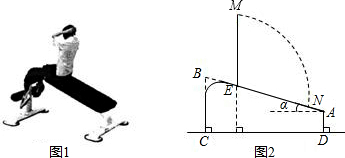
 如圖a和b是相交于點O的兩條公路,A,B是兩個加油站,現準備在∠AOB的內部建一個油庫,要求油庫的位置點P既到A,B兩個加油站的距離相等,又到兩條公路a,b的距離相等,試用尺規作圖作出點P.
如圖a和b是相交于點O的兩條公路,A,B是兩個加油站,現準備在∠AOB的內部建一個油庫,要求油庫的位置點P既到A,B兩個加油站的距離相等,又到兩條公路a,b的距離相等,試用尺規作圖作出點P.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com