
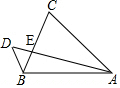
 如圖.在△ABC中,AB=AC,D為△ABC外一點,連結AD,交BC于點E,連結DB,若∠C=∠D,AE=8,DE=2.求AC的長.
如圖.在△ABC中,AB=AC,D為△ABC外一點,連結AD,交BC于點E,連結DB,若∠C=∠D,AE=8,DE=2.求AC的長. 分析 由AB=AC知∠ABE=∠C,結合∠C=∠D得∠ABE=∠D,利用∠BAE=∠DAB證△ABE∽△ADB得$\frac{AB}{AD}=\frac{AE}{AB}$,從而得出AB=AC=4$\sqrt{5}$.
解答 解:如圖,
∵AB=AC,
∴∠ABE=∠C,
∵∠C=∠D,
∴∠ABE=∠D,
又∵∠BAE=∠DAB,
∴△ABE∽△ADB,
∴$\frac{AB}{AD}=\frac{AE}{AB}$,即$\frac{AB}{8+2}$=$\frac{8}{AB}$,
解得:AB=4$\sqrt{5}$,
∴AC=AB=4$\sqrt{5}$.
點評 本題主要考查相似三角形的判定與性質及等腰三角形的性質,在判定兩個三角形相似時,應注意利用圖形中已有的公共角、公共邊等隱含條件,以充分發揮基本圖形的作用,尋找相似三角形的一般方法是通過作平行線構造相似三角形;或依據基本圖形對圖形進行分解、組合;或作輔助線構造相似三角形,判定三角形相似的方法有事可單獨使用,有時需要綜合運用,無論是單獨使用還是綜合運用,都要具備應有的條件方可.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
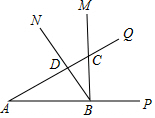 如圖,∠PAQ=∠MBN=30°,∠MBN的頂點B在射線AP上,射線BM和射線BN分別交射線AQ于點C、D,當∠MBN繞點B轉動時.若AB=2$\sqrt{3}$,則CA•CD的最小值是( )
如圖,∠PAQ=∠MBN=30°,∠MBN的頂點B在射線AP上,射線BM和射線BN分別交射線AQ于點C、D,當∠MBN繞點B轉動時.若AB=2$\sqrt{3}$,則CA•CD的最小值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 4 | D. | 12 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
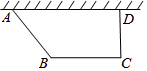 如圖,要建造一個直角梯形的花圃,要求AD邊靠墻,CD⊥AD,AB:CD=5:4,另外三邊的和為20米,設AB的長為5x米
如圖,要建造一個直角梯形的花圃,要求AD邊靠墻,CD⊥AD,AB:CD=5:4,另外三邊的和為20米,設AB的長為5x米查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
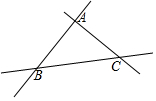 如圖是三條兩兩相交的筆直公路,現欲修建一個加油站,使它到三條公路的距離相等,這個加油站應建在( )
如圖是三條兩兩相交的筆直公路,現欲修建一個加油站,使它到三條公路的距離相等,這個加油站應建在( )| A. | △ABC三邊的中線的交點上 | B. | △ABC三邊垂直平分線的交點上 | ||
| C. | △ABC三條邊高的交點上 | D. | △ABC三內角平分線的交點上 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com