
 已知△ABC為等邊三角形,點D、E分別在線段BC、CA上,且CE=BD.直線AD與BE相交于點M.求證:
已知△ABC為等邊三角形,點D、E分別在線段BC、CA上,且CE=BD.直線AD與BE相交于點M.求證:分析 ①根據等邊三角形性質得出AB=BC,∠ABD=∠C=60°,再根據SAS可得△ABD≌△BCE;
②根據全等三角形的性質推出∠BAD=∠CBE,再通過三角形外角性質即可求出∠AME的度數.
解答 證明:①∵△ABC為等邊三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴AD=BE.
②∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠AME=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.
點評 本題主要考查了等邊三角形的性質以及全等三角形的判定及性質問題,能求出△ABD≌△BCE是解此題的關鍵.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
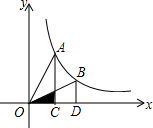 如圖是一個反比例函數(x>0)的圖象,點A(2,4)在圖象上,AC⊥x軸于C,當點A運動到圖象上的點B(4,2)處,BD⊥x軸于D,△AOC與△BOD重疊部分的面積為( )
如圖是一個反比例函數(x>0)的圖象,點A(2,4)在圖象上,AC⊥x軸于C,當點A運動到圖象上的點B(4,2)處,BD⊥x軸于D,△AOC與△BOD重疊部分的面積為( )| A. | 1 | B. | 2 | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知:在△ABC中,AC=BC=4,∠ACB=120°,將一塊足夠大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如圖放置,頂點P在線段AB上滑動,三角尺的直角邊PM始終經過點C,并且與CB的夾角∠PCB=α,斜邊PN交AC于點D.
如圖,已知:在△ABC中,AC=BC=4,∠ACB=120°,將一塊足夠大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如圖放置,頂點P在線段AB上滑動,三角尺的直角邊PM始終經過點C,并且與CB的夾角∠PCB=α,斜邊PN交AC于點D.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com