
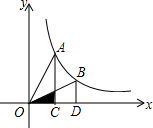
 如圖是一個反比例函數(x>0)的圖象,點A(2,4)在圖象上,AC⊥x軸于C,當點A運動到圖象上的點B(4,2)處,BD⊥x軸于D,△AOC與△BOD重疊部分的面積為( )
如圖是一個反比例函數(x>0)的圖象,點A(2,4)在圖象上,AC⊥x軸于C,當點A運動到圖象上的點B(4,2)處,BD⊥x軸于D,△AOC與△BOD重疊部分的面積為( )| A. | 1 | B. | 2 | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
分析 根據題意可以得到點C和點D的坐標,然后根據AC⊥x軸于C,BD⊥x軸于D可以得到△OCE∽△ODB,然后根據對應邊的比相等,可以求出CE的長,從而可以求得,△AOC與△BOD重疊部分的面積.
解答 解:如下圖所示: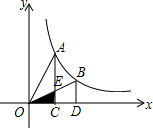
∵點A(2,4),點B(4,2),AC⊥x軸于C,BD⊥x軸于D,
∴點C的坐標為(2,0),點D的坐標為(4,0),AC∥BD,
∴△OCE∽△ODB,
∴$\frac{OC}{OD}=\frac{CE}{DB}$,
即$\frac{2}{4}=\frac{CE}{2}$
解得CE=1,
∴${S}_{△OCE}=\frac{OC•CE}{2}=\frac{2×1}{2}=1$,
即△AOC與△BOD重疊部分的面積為1.
故選A.
點評 本題考查相似三角形的判定和性質,解題的關鍵是明確相似三角形的判定和性質是什么,找出所求問題需要的條件.


科目:初中數學 來源: 題型:填空題
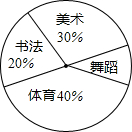 某校為了解學生的課余愛好,對全校1200名學生進行抽樣調查,并把調查結果制成如圖所示的統計圖,由圖可知,該校喜歡舞蹈的學生大約有120名.
某校為了解學生的課余愛好,對全校1200名學生進行抽樣調查,并把調查結果制成如圖所示的統計圖,由圖可知,該校喜歡舞蹈的學生大約有120名.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知△ABC為等邊三角形,點D、E分別在線段BC、CA上,且CE=BD.直線AD與BE相交于點M.求證:
已知△ABC為等邊三角形,點D、E分別在線段BC、CA上,且CE=BD.直線AD與BE相交于點M.求證:查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (-2,1) | B. | (2,1) | C. | (2,-1) | D. | (1,2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com