Question

17．如圖，已知：在△ABC中，AC=BC=4，∠ACB=120°，將一塊足夠大的直角三角尺PMN（∠M=90°，∠MPN=30°）按如圖放置，頂點P在線段AB上滑動，三角尺的直角邊PM始終經過點C，并且與CB的夾角∠PCB=α，斜邊PN交AC于點D．
（1）當PN∥BC時，判斷△ACP的形狀，并說明理由；
（2）點P在滑動時，當AP長為多少時，△ADP與△BPC全等，為什么？
（3）點P在滑動時，△PCD的形狀可以是等腰三角形嗎？若可以，請求出夾角α的大小；若不可以，請說明理由．

Answer 1

分析 （1）△ACP為直角三角形，理由為：由PN與BC平行，得到一對內錯角相等，求出∠ACP為直角，即可得證；
（2）當AP=4時，△ADP與△BPC全等，理由為：根據CA=CB，且∠ACB度數，求出∠A與∠B度數，再由外角性質得到∠α=∠APD，根據AP=BC，利用ASA即可得證；
（3）點P在滑動時，△PCD的形狀可以是等腰三角形，分三種情況考慮：當PC=PD；PD=CD；PC=CD，分別求出夾角α的大小即可．

解答 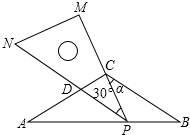解：（1）△ACP是直角三角形，理由為：
當PN∥BC時，∠α=∠NPM=30°，
又∵∠ACB=120°，
∴∠ACP=120°-30°=90°，
∴△ACP是直角三角形；
（2）當AP=4時，△ADP≌△BPC，
理由為：∵∠ACB=120°，CA=CB，
∴∠A=∠B=30°，
又∵∠APC是△BPC的一個外角，
∴∠APC=∠B+∠α=30°+∠α，
∵∠APC=∠DPC+∠APD=30°+∠APD，
∴∠α=∠APD，
又∵AP=BC=4，
∴△ADP≌△BPC；
（3）△PCD的形狀可以是等腰三角形，
則∠PCD=120°-α，∠CPD=30°，
①當PC=PD時，△PCD是等腰三角形，
∴∠PCD=∠PDC=$\frac{180°-30°}{2}$=75°，即120°-α=75°，
∴∠α=45°；
②當PD=CD時，△PCD是等腰三角形，
∴∠PCD=∠CPD=30°，即120°-α=30°，
∴α=90°；
③當PC=CD時，△PCD是等腰三角形，
∴∠CDP=∠CPD=30°，
∴∠PCD=180°-2×30°=120°，
即120°-α=120°，
∴α=0°，
此時點P與點B重合，點D和A重合，
綜合所述：當α=45°或90°或0°時，△PCD是等腰三角形．

點評 此題考查了全等三角形的判定與性質，等腰三角形的判定，外角性質，直角三角形的性質，熟練掌握全等三角形的判定與性質是解本題的關鍵．