Question

12．等邊三角形ABC的邊長為4cm，點D從點C出發沿CA向A運動，點E從B出發沿AB的延長線BF向右運動，已知點D、E都以每秒0.5cm的速度同時開始運動，運動過程中DE與BC相交于點P．
（1）運動幾秒后，△ADE為直角三角形？
（2）在點D、E運動時，線段PD與線段PE相等嗎？如果相等，給以證明；如不相等，說明理由．

Answer 1

分析 （1）根據等邊三角形的性質和直角三角形的性質求出∠AED=30°，根據直角三角形的性質列出關系式，計算即可；
（2）過D點作DH∥AF交BC于點H，證明△DGP≌△EBP，根據全等三角形的性質定理證明即可．

解答 解：（1）∵△ABC是等邊三角形，
∴∠A=60°，
△ADE為直角三角形時，∠ADE=90°，
則∠AED=30°，
∴AD=$\frac{1}{2}$AE，即4-0.5t=$\frac{1}{2}$（4+0.5t），
t=$\frac{8}{3}$，
答：運動$\frac{8}{3}$秒后，△ADE為直角三角形；
（2）PD=PE．
證明：過D點作DH∥AF交BC于點H，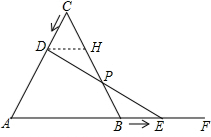
則△CDH為等邊三角形，∠HDP=∠PEB，
∴DH=DC，又DC=BE，
∴DH=BE，
在△DGP和△EBP中，
$\left\{\begin{array}{l}{∠HDP=∠BEP}\\{∠DPH=∠EPB}\\{DH=BE}\end{array}\right.$，
∴△DGP≌△EBP，
∴PD=PE．

點評 本題考查的是全等三角形的判定和性質、等邊三角形的性質，掌握三角形全等是判判定定理、平行線的性質、等邊三角形的判定定理和性質定理是解題的關鍵．