Question

2．某地因持續高溫干旱，村民飲水困難，鎮政府組織村民組成水源行動小組到村鎮周邊找水．某村民在山洞C里發現了暗河（如圖所示），經勘察，在山洞的西面有一條南北走向的公路連接著A，B兩村莊，山洞C位于A村莊南偏東30°方向，且位于B村莊南偏東60°方向．為方便A，B兩村莊的村民取水，準備從山洞C處向公路AB緊急修建一條最近的簡易公路CD，現已知A，B兩村莊相距6千米．
（1）求這條最近的簡易公路CD的長（精確到0.1千米）？
（2）現由甲、乙兩施工隊共同合作修建這條公路，已知甲施工隊修建2千米后，由乙施工隊繼續修建，乙施工隊每天施工的速度是甲施工隊每天施工速度的1.6倍，8天后，公路CD正式通車．求甲、乙兩施工隊每天修建公路多少千米？
（參考數據：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

Answer 1

分析 （1）過C作CD⊥AB于D，設CD=x．在直角△ACD與直角△BCD中，根據三角函數即可用x表示出AD于BD的長，根據AB=AD-BD，即得到關于x的方程．解方程求解即可；
（2）根據題意列出分式方程，解方程即可．

解答 解：（1）如圖：過C作CD⊥AB于D，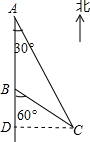
設CD=x，
在Rt△ADC中，∠ADC=90°，∠A=30°，
tan∠A=$\frac{CD}{AD}$，
則AD=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x，
在Rt△BDC中，∠BDC=90°，∠DBC=60°，
tan∠DBC=$\frac{CD}{BD}$，
則BD=$\frac{\sqrt{3}}{3}$x，
∵AB=AD-BD=6，
∴$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=6，
解得x=3$\sqrt{3}$≈5.2．
答：這條最近的簡易公路CD的長約為 5.2千米；
（2）設甲施工隊每天修建公路x千米，則乙施工隊每天修建公路1.6x千米．
由題意得，$\frac{2}{x}$+$\frac{5.2-2}{1.6x}$=8，
解得x=0.5，
經檢驗，x=0.5是原方程的解，
1.6x=0.8．
答：甲施工隊每天修建公路0.5千米，則乙施工隊每天修建公路0.8千米．

點評 本題考查的是解直角三角形的應用-方向角問題和分式方程的應用，正確作出輔助線、熟記銳角三角函數的定義、根據題意列出分式方程是解題的關鍵．