
 如圖,有一塊直角三角形紙片ABC,∠C=90°.兩直角邊AC=6cm,BC=8cm,現將該紙片沿直線AD折疊,使點C落在斜邊AB上的點E處,則折痕AD=3$\sqrt{5}$cm.
如圖,有一塊直角三角形紙片ABC,∠C=90°.兩直角邊AC=6cm,BC=8cm,現將該紙片沿直線AD折疊,使點C落在斜邊AB上的點E處,則折痕AD=3$\sqrt{5}$cm. 分析 先根據勾股定理求得AB的長,再根據折疊的性質求得AE,BE的長,從而利用勾股定理可求得CD的長,然后根據勾股定理即可求得AD.
解答 解:∵AC=6cm,BC=8cm,∠C=90°
∴AB=10cm,
∵AE=6cm(折疊的性質),
∴BE=4cm,
設CD=x,
則在Rt△DEB中,
42+x2=(8-x)2,
∴x=3cm.
∴CD=3cm,
在Rt△ACD中,AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=3$\sqrt{5}$cm.
故答案為3$\sqrt{5}$.
點評 本題考查了翻折變換的性質,勾股定理的應用,熟記性質并表示出Rt△DEB的三邊,然后利用勾股定理列出方程是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 已知:如圖,在△ABC中,AB=AC,以AC為直徑的⊙O交AB于點M,交BC于點N,連接AN,過點C的切線交AB的延長線于點P.
已知:如圖,在△ABC中,AB=AC,以AC為直徑的⊙O交AB于點M,交BC于點N,連接AN,過點C的切線交AB的延長線于點P.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 操作探究:已知在紙面上有一數軸(如圖所示),
操作探究:已知在紙面上有一數軸(如圖所示),查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,已知∠A=n°,若P1點是∠ABC和外角∠ACE的角平分線的交點,P2點是∠P1BC和外角∠P1CE的角平分線的交點,P3點是∠P2BC和外角∠P2CE的交點…依此類推,則∠Pn=( )
如圖,已知∠A=n°,若P1點是∠ABC和外角∠ACE的角平分線的交點,P2點是∠P1BC和外角∠P1CE的角平分線的交點,P3點是∠P2BC和外角∠P2CE的交點…依此類推,則∠Pn=( )| A. | $\frac{n°}{2n}$ | B. | $\frac{n°}{2^n}$ | C. | $\frac{n°}{{{2^{n-1}}}}$ | D. | $\frac{n°}{2(n-1)}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
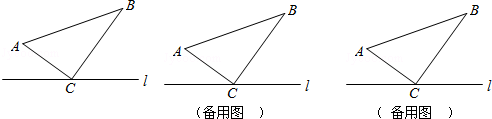
 某地因持續高溫干旱,村民飲水困難,鎮政府組織村民組成水源行動小組到村鎮周邊找水.某村民在山洞C里發現了暗河(如圖所示),經勘察,在山洞的西面有一條南北走向的公路連接著A,B兩村莊,山洞C位于A村莊南偏東30°方向,且位于B村莊南偏東60°方向.為方便A,B兩村莊的村民取水,準備從山洞C處向公路AB緊急修建一條最近的簡易公路CD,現已知A,B兩村莊相距6千米.
某地因持續高溫干旱,村民飲水困難,鎮政府組織村民組成水源行動小組到村鎮周邊找水.某村民在山洞C里發現了暗河(如圖所示),經勘察,在山洞的西面有一條南北走向的公路連接著A,B兩村莊,山洞C位于A村莊南偏東30°方向,且位于B村莊南偏東60°方向.為方便A,B兩村莊的村民取水,準備從山洞C處向公路AB緊急修建一條最近的簡易公路CD,現已知A,B兩村莊相距6千米.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com