
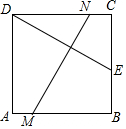
 如圖,將邊長為8厘米的正方形紙片ABCD折疊,使點D落在BC邊中點E處,點A落在點F處,折痕為MN,則線段MN的長是4$\sqrt{5}$cm.
如圖,將邊長為8厘米的正方形紙片ABCD折疊,使點D落在BC邊中點E處,點A落在點F處,折痕為MN,則線段MN的長是4$\sqrt{5}$cm. 分析 過點M作MF⊥CD于F,根據(jù)翻折變換的性質(zhì)可得MN⊥DE,然后求出∠MNF=∠DEC,再利用“角角邊”證明△DCE和△MFN全等,根據(jù)全等三角形對應(yīng)邊相等可得MN=DE,再利用勾股定理列式求出DE,從而得解.
解答 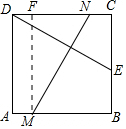 解:如圖,過點M作MF⊥CD于F,
解:如圖,過點M作MF⊥CD于F,
易得四邊形AMFD是矩形,
所以,MF=AD,
由翻折變換的性質(zhì)得MN⊥DE,
∵∠CDE+∠MNF=90°,
∠CDE+∠DEC=90°,
∴∠MNF=∠DEC,
∵四邊形ABCD是正方形,
∴AD=CD,
∴MF=CD,
在△DCE和△MFN中,$\left\{\begin{array}{l}{∠MNF=∠DEC}\\{∠MFN=∠C=90°}\\{MF=CD}\end{array}\right.$,
∴△DCE≌△MFN(AAS),
∴MN=DE,
∵點E是BC的中點,
∴CE=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4cm,
在Rt△CDE中,由勾股定理得,DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$cm,
所以,MN的長為4$\sqrt{5}$cm.
故答案為:4$\sqrt{5}$cm.
點評 本題考查了翻折變換的性質(zhì),正方形的性質(zhì),全等三角形的判定與性質(zhì),作輔助線構(gòu)造出全等三角形是解題的關(guān)鍵,也是本題的難點.


 舉一反三單元同步過關(guān)卷系列答案
舉一反三單元同步過關(guān)卷系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
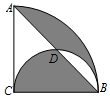 如圖,在半徑為2,圓心角為90°的扇形內(nèi),以BC為直徑作半圓,交弦AB于點D,連接CD,則陰影部分的面積為( )
如圖,在半徑為2,圓心角為90°的扇形內(nèi),以BC為直徑作半圓,交弦AB于點D,連接CD,則陰影部分的面積為( )| A. | π-1 | B. | 2π-1 | C. | 2π-2 | D. | π-2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. |  | B. | 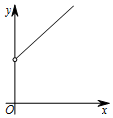 | C. | 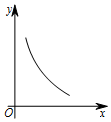 | D. |  |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 底邊對應(yīng)相等的兩個等腰三角形全等 | |
| B. | 腰對應(yīng)相等的兩個等腰三角形全等 | |
| C. | 斜邊對應(yīng)相等的兩個直角三角形全等 | |
| D. | 面積相等的兩個等邊三角形全等 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
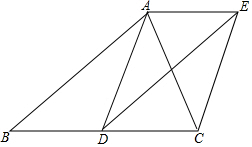 如圖所示,已知AD是△ABC的中線,DE∥AB,且DE=AB,連結(jié)AE,EC,求證:四邊形ADCE是平行四邊形.
如圖所示,已知AD是△ABC的中線,DE∥AB,且DE=AB,連結(jié)AE,EC,求證:四邊形ADCE是平行四邊形.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{5}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
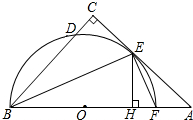 如圖,在△ABC中,∠C=90°,∠ABC的平分線交AC于點E,過點E作BE的垂線交AB于點F,⊙O是△BEF的外接圓.
如圖,在△ABC中,∠C=90°,∠ABC的平分線交AC于點E,過點E作BE的垂線交AB于點F,⊙O是△BEF的外接圓.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com