Question

5．如圖①，△ABC是邊長為6cm的等邊三角形，點M，N分別從點A，B同時出發，沿邊AB，BC運動，且它們的速度都為1cm/s．設點M的運動時間為t （s）．
（1）在圖①中，畫出點M、N并連接MN，當t=2或4時，△BMN是直角三角形；
（2）如圖②，連接AN、CM，相交于點P，當t=3時，△ABN≌△CBM；
（3）圖②中，點M，N在運動的過程中，∠CPN的度數會發生變化嗎？若變化，則說明理由；若不變，請求出它的度數．

Answer 1

分析 （1）分兩種情況：①如圖1，當∠BNM=90°時，∠BMN=30°，則BM=2BN，②如圖2，當∠BMN=90°時，∠BNM=30°，BN=2BM，分別列式可求得t的值；
（2）如圖3，當BM=BN時，△ABN≌△CBM，則AM=BM，所以t=6-t，解出即可；
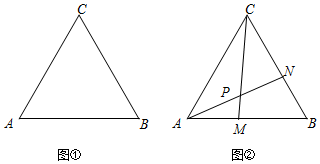
（3）如圖4，∠CPN的度數不會發生變化，都等于60°，證明△CAM≌△ABN，再利用外角定理可以得出結論．

解答 解：（1）由題意得：AM=BN=t，則BM=6-t
當△BMN是直角三角形時，有兩種情況：
①如圖1，當∠BNM=90°時，
∵△ABC是等邊三角形，
∴∠B=60°，
∴∠BMN=90°-60°=30°，
∴BM=2BN，
∴6-t=2t，
t=2；
②如圖2，當∠BMN=90°時，
∵∠B=60°，
∴∠BNM=30°，
∴BN=2BM，
∴t=2（6-t），
t=4，
綜上所述，當t=2或4時，△BMN是直角三角形；
故答案為：2或4；
（2）如圖3，∵AB=BC，∠B=∠B，
∴當BM=BN時，△ABN≌△CBM，
∵AM=BN，
∴AM=BM，
∴t=6-t，
t=3，
∴當t=3時，△ABN≌△CBM，
故答案為：3；
（3）點M，N在運動的過程中，∠CPN的度數不會發生變化，都等于60°，理由是：
如圖4，
在△CAM和△ABN中，
∵$\left\{\begin{array}{l}{AC=AB}\\{∠CAB=∠ABC=60°}\\{AM=BN}\end{array}\right.$，
∴△CAM≌△ABN（SAS），
∴∠ACM=∠BAN，
∵∠BAN+∠CAN=∠CAB=60°，
∴∠ACM+∠CAN=60°，
∵∠CPN=∠ACM+∠CAN，
∴∠CPN=60°．

點評 本題考查了等邊三角形、全等三角形的性質和判定以及動點運動問題，難度適中，是中考常考題型；在動點問題中，如圖速度相等，時間相等，則路程相等；同時在第1問中采用了分類討論的思想，容易丟解，要注意．