
 如圖,一次函數(shù)y=kx+b與反比例函數(shù)y=$\frac{m}{x}$圖象交于A,B兩點(diǎn),與x軸交于點(diǎn)C(-2,0),點(diǎn)A的橫坐標(biāo)為1,S△AOC=2.
如圖,一次函數(shù)y=kx+b與反比例函數(shù)y=$\frac{m}{x}$圖象交于A,B兩點(diǎn),與x軸交于點(diǎn)C(-2,0),點(diǎn)A的橫坐標(biāo)為1,S△AOC=2.分析 (1)根據(jù)C的坐標(biāo)和S△AOC=2求得A的坐標(biāo),然后根據(jù)待定系數(shù)法即可求得一次函數(shù)及反比例函數(shù)的表達(dá)式;
(2)聯(lián)立方程求得B的坐標(biāo),根據(jù)圖象即可求得.
解答 解:(1)∵C(-2,0),S△AOC=2.
∴OC=2,$\frac{1}{2}$OC•|yA|=2,
∴|yA|=2,
∵點(diǎn)A在第一象限,
∴A(1,2),
∵A點(diǎn)在反比例函數(shù)y=$\frac{m}{x}$圖象上,
∴m=1×2=2,
∵一次函數(shù)y=kx+b經(jīng)過(guò)A(1,2),C(-2,0),
∴$\left\{\begin{array}{l}{k+b=2}\\{-2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
∴一次函數(shù)的解析式為y=$\frac{2}{3}$x+$\frac{4}{3}$,反比例函數(shù)的解析式為y=$\frac{2}{x}$;
(2)∵解$\left\{\begin{array}{l}{y=\frac{2}{3}x+\frac{4}{3}}\\{y=\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-3}\\{y=-\frac{2}{3}}\end{array}\right.$,
∴B(-3,-$\frac{2}{3}$),
∴反比例函數(shù)值大于一次函數(shù)值時(shí)x的取值范圍:x<-3或0<x<1.
點(diǎn)評(píng) 本題考查了反比例函數(shù)與一次函數(shù)的交點(diǎn)問(wèn)題:反比例函數(shù)與一次函數(shù)的交點(diǎn)坐標(biāo)同時(shí)滿(mǎn)足兩個(gè)函數(shù)的解析式.也考查了三角形面積公式、待定系數(shù)法求函數(shù)的解析式.


 53天天練系列答案
53天天練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 周長(zhǎng)相等的兩個(gè)等邊三角形全等 | B. | 斜邊相等的兩個(gè)直角三角形全等 | ||
| C. | 面積相等的兩個(gè)三角形全等 | D. | 腰長(zhǎng)相等的兩個(gè)等腰三角形全等 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 已知:如圖,在△ABC中,∠A=30°,∠B=60°
已知:如圖,在△ABC中,∠A=30°,∠B=60°查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,在△ABC中,AD是BC邊上的中線.
如圖,在△ABC中,AD是BC邊上的中線.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,長(zhǎng)方形OABC中,O為平面直角坐標(biāo)系的原點(diǎn),A點(diǎn)的坐標(biāo)為(4,0),C點(diǎn)的坐標(biāo)為(0,10),點(diǎn)B在第一象限內(nèi).D為OC的中點(diǎn).
如圖,長(zhǎng)方形OABC中,O為平面直角坐標(biāo)系的原點(diǎn),A點(diǎn)的坐標(biāo)為(4,0),C點(diǎn)的坐標(biāo)為(0,10),點(diǎn)B在第一象限內(nèi).D為OC的中點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
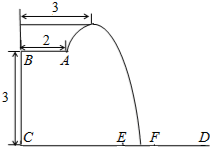 在2014年仁川亞運(yùn)會(huì)上中國(guó)隊(duì)包攬了跳水所有項(xiàng)目的金牌.過(guò)去十一屆亞運(yùn)會(huì)的跳水金牌也全部歸于中國(guó)跳水隊(duì)!優(yōu)秀成績(jī)的取得離不開(kāi)艱辛的訓(xùn)練.某跳水運(yùn)動(dòng)員在進(jìn)行一次跳水訓(xùn)練時(shí),身體(看成一點(diǎn))在空中的運(yùn)動(dòng)路線是如圖所示的一條拋物線.已知跳板AB長(zhǎng)為2米,跳板距水面CD高BC為3米,為安全和空中姿勢(shì)優(yōu)美,訓(xùn)練時(shí)跳水曲線在離起跳點(diǎn)水平距離1米時(shí)達(dá)到距水面最大高度4米,現(xiàn)以CD為橫軸,CB為縱軸建立直角坐標(biāo)系.
在2014年仁川亞運(yùn)會(huì)上中國(guó)隊(duì)包攬了跳水所有項(xiàng)目的金牌.過(guò)去十一屆亞運(yùn)會(huì)的跳水金牌也全部歸于中國(guó)跳水隊(duì)!優(yōu)秀成績(jī)的取得離不開(kāi)艱辛的訓(xùn)練.某跳水運(yùn)動(dòng)員在進(jìn)行一次跳水訓(xùn)練時(shí),身體(看成一點(diǎn))在空中的運(yùn)動(dòng)路線是如圖所示的一條拋物線.已知跳板AB長(zhǎng)為2米,跳板距水面CD高BC為3米,為安全和空中姿勢(shì)優(yōu)美,訓(xùn)練時(shí)跳水曲線在離起跳點(diǎn)水平距離1米時(shí)達(dá)到距水面最大高度4米,現(xiàn)以CD為橫軸,CB為縱軸建立直角坐標(biāo)系.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com