
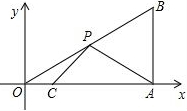
 如圖,在平面直角坐標系中,Rt△OAB的直角頂點A在x軸的正半軸上,頂點B的縱坐標為2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,點P是斜邊DB上的一個動點,則△PAC的周長的最小值為2$\sqrt{7}$+4.
如圖,在平面直角坐標系中,Rt△OAB的直角頂點A在x軸的正半軸上,頂點B的縱坐標為2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,點P是斜邊DB上的一個動點,則△PAC的周長的最小值為2$\sqrt{7}$+4.分析 作A關于OB的對稱點D,連接CD交OB于P,連接AP,過D作DN⊥OA于N,則此時PA+PC的值最小,求出AM,求出AD,求出DN、CN,根據勾股定理求出CD,即可得出答案.
解答 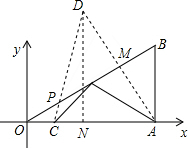 解:作A關于OB的對稱點D,連接CD交OB于P,連接AP,過D作DN⊥OA于N,則此時PA+PC的值最小,
解:作A關于OB的對稱點D,連接CD交OB于P,連接AP,過D作DN⊥OA于N,則此時PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵頂點B的縱坐標為2$\sqrt{3}$,∠B=60°,
∴AB=2$\sqrt{3}$,OA=6,由勾股定理得:OB=4$\sqrt{3}$,
由三角形面積公式得:$\frac{1}{2}$×OA×AB=$\frac{1}{2}$×OB×AM,
∴AM=3,
∴AD=2×3=6,
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴∠NDA=30°,
∴AN=$\frac{1}{2}$AD=3,由勾股定理得:DN=3$\sqrt{3}$,
∵C(1,0),
∴CN=AC-AN=4-3=1,
在Rt△DNC中,由勾股定理得:DC=$\sqrt{{1}^{2}+(3\sqrt{3})^{2}}$=2$\sqrt{7}$,
即PA+PC的最小值是2$\sqrt{7}$,
∴△PAC周長的最小值為:2$\sqrt{7}$+4.
故答案為:2$\sqrt{7}$+4.
點評 本題考查了軸對稱-最短路線問題,三角形的內角和定理,勾股定理,含30度角的直角三角形性質的應用,關鍵是求出P點的位置,題目比較好,難度適中.


 單元期中期末卷系列答案
單元期中期末卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
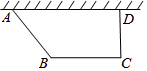 如圖,要建造一個直角梯形的花圃,要求AD邊靠墻,CD⊥AD,AB:CD=5:4,另外三邊的和為20米,設AB的長為5x米
如圖,要建造一個直角梯形的花圃,要求AD邊靠墻,CD⊥AD,AB:CD=5:4,另外三邊的和為20米,設AB的長為5x米查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)計算:(-$\frac{1}{2}$)-1+$\sqrt{3}$tan30°-sin245°
(1)計算:(-$\frac{1}{2}$)-1+$\sqrt{3}$tan30°-sin245°查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
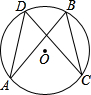
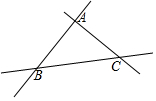 如圖是三條兩兩相交的筆直公路,現欲修建一個加油站,使它到三條公路的距離相等,這個加油站應建在( )
如圖是三條兩兩相交的筆直公路,現欲修建一個加油站,使它到三條公路的距離相等,這個加油站應建在( )| A. | △ABC三邊的中線的交點上 | B. | △ABC三邊垂直平分線的交點上 | ||
| C. | △ABC三條邊高的交點上 | D. | △ABC三內角平分線的交點上 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com