
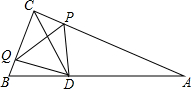
 如圖,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=3cm,∠ABC的平分線交于點(diǎn)D,動(dòng)點(diǎn)P,Q從點(diǎn)C同時(shí)出發(fā),點(diǎn)P以1cm/s的速度沿射線CA方向運(yùn)動(dòng),點(diǎn)Q以2cm/s的速度沿射線CB方向運(yùn)動(dòng),當(dāng)點(diǎn)P到達(dá)點(diǎn)A時(shí),P、Q兩點(diǎn)同時(shí)停止運(yùn)動(dòng),設(shè)點(diǎn)P的運(yùn)動(dòng)時(shí)間為t(s),連接PQ,PD,QD.
如圖,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=3cm,∠ABC的平分線交于點(diǎn)D,動(dòng)點(diǎn)P,Q從點(diǎn)C同時(shí)出發(fā),點(diǎn)P以1cm/s的速度沿射線CA方向運(yùn)動(dòng),點(diǎn)Q以2cm/s的速度沿射線CB方向運(yùn)動(dòng),當(dāng)點(diǎn)P到達(dá)點(diǎn)A時(shí),P、Q兩點(diǎn)同時(shí)停止運(yùn)動(dòng),設(shè)點(diǎn)P的運(yùn)動(dòng)時(shí)間為t(s),連接PQ,PD,QD.分析 (1)由題意PC=t,QC=2t,在Rt△PQC中,根據(jù)PQ=$\sqrt{P{C}^{2}+C{Q}^{2}}$,即可解決問(wèn)題.
(2)如圖1中,作DE⊥AC于E,DF⊥BC于F.首先證明四邊形CFDE是正方形,設(shè)正方形的邊長(zhǎng)為x,由DE∥BC,可得$\frac{DE}{BC}$=$\frac{AE}{AC}$,即$\frac{x}{3}$=$\frac{6-x}{6}$,解方程即可解決問(wèn)題.
(3)①如圖2中,作MH⊥AC于M,MG⊥BC于G,則四邊形CGMH是正方形,設(shè)邊長(zhǎng)為y,分兩種情形a、當(dāng)0<t≤1.5時(shí),重疊部分是△PQD.b、當(dāng)1.5<t<3時(shí),重疊部分是△PKD,分別求解即可.
②分三種情形討論即可.a(chǎn)、當(dāng)0<t≤1.5時(shí),重疊部分是△PQD.b、當(dāng)1.5<t<3時(shí),重疊部分是△PKD,分別求解即可.c、當(dāng)t≥3時(shí),分別利用二次函數(shù)的性質(zhì)即可解決問(wèn)題.
解答 解:(1)由題意PC=t,QC=2t,
在Rt△PQC中,PQ=$\sqrt{P{C}^{2}+C{Q}^{2}}$=$\sqrt{{t}^{2}+(2t)^{2}}$=$\sqrt{5}$t.
(2)如圖1中,作DE⊥AC于E,DF⊥BC于F.
∵∠ACB=90°,DC平分∠ACB,
∴∠DCE=∠DCF=∠DCE=∠CDF=45°,
∴EC=ED,F(xiàn)C=FD,
∵DF⊥BC,DE⊥AC,
∴DE=DF,
∴DE=DF=CF=EC,
∴四邊形CFDE是菱形,∠ECF=90°,
∴四邊形CFDE是正方形,設(shè)正方形的邊長(zhǎng)為x,
∵DE∥BC,
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$,
∴$\frac{x}{3}$=$\frac{6-x}{6}$,
∴x=2.
∴點(diǎn)D到AC的距離為2.
(3)①如圖2中,作MH⊥AC于M,MG⊥BC于G,則四邊形CGMH是正方形,設(shè)邊長(zhǎng)為y,
∵M(jìn)H∥CQ,
∴$\frac{MH}{CQ}$=$\frac{PH}{PC}$,
∴$\frac{y}{2t}$=$\frac{t-y}{t}$,
∴y=$\frac{2}{3}$t,
當(dāng)0<t≤1.5時(shí),重疊部分是△PQD,
∴S=(S△CQD-S△CQM)+(S△CPD-S△CPM)=$\frac{1}{2}$•2t(2-$\frac{2}{3}$t)+$\frac{1}{2}$•t•(2-$\frac{2}{3}$t)=$\frac{3}{2}$t(2-$\frac{2}{3}$t)=3t-t2.
如圖3中,作PT∥AB交BC于T,QR⊥AB于R.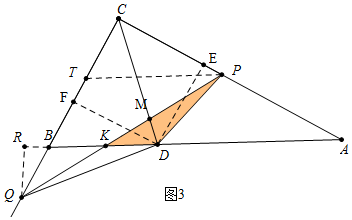
∵$\frac{PT}{AB}$=$\frac{PC}{AC}$=$\frac{CT}{BC}$,
∴$\frac{PT}{3\sqrt{5}}$=$\frac{t}{6}$=$\frac{CT}{3}$,
∴PT=$\frac{\sqrt{5}}{2}$t,CT=$\frac{1}{2}$t,
∵BK∥PT,
∴$\frac{BK}{PT}$=$\frac{QB}{QT}$,
∴$\frac{BK}{\frac{\sqrt{5}}{2}t}$=$\frac{2t-3}{2t-\frac{1}{2}t}$,
∴BK=$\frac{\sqrt{5}}{3}$(2t-3),
當(dāng)點(diǎn)K與點(diǎn)D重合時(shí),$\frac{\sqrt{5}}{3}$(2t-3)=$\sqrt{5}$,解得t=3,
∴KD=$\sqrt{5}$-$\frac{\sqrt{5}}{3}$(2t-3)=2$\sqrt{5}$-$\frac{2}{3}$$\sqrt{5}$t,
由△QRB∽△DFB,可得$\frac{QR}{DF}$=$\frac{BQ}{DB}$,
∴$\frac{QR}{2}$=$\frac{2t-3}{\sqrt{5}}$,
∴QR=$\frac{2\sqrt{5}}{5}$(2t-3),
∴當(dāng)1.5<t<3時(shí),重疊部分是△PKD,
S=S△PDQ-S△QDK=3t-t2-$\frac{1}{2}$•(2$\sqrt{5}$-$\frac{2}{3}$$\sqrt{5}$t)•$\frac{2\sqrt{5}}{5}$(2t-3)=$\frac{1}{3}$t2-3t+6.
綜上所述,S=$\left\{\begin{array}{l}{3t-{t}^{2}}&{(0<t≤1.5)}\\{\frac{1}{3}{t}^{2}-3t+6}&{(1.5<t<3)}\end{array}\right.$.
②由①可知,當(dāng)0<t≤1.5時(shí),S隨t的增大而增大.
如圖4中,
當(dāng)t≥3時(shí),重疊部分是△PDK,S=$\frac{1}{2}$•DK•PH=$\frac{1}{2}$•[$\frac{\sqrt{5}}{3}$(2t-3)-$\sqrt{5}$]•$\frac{\sqrt{5}}{5}$(6-t)=-$\frac{1}{3}$t2+3t-6,
∵-$\frac{1}{3}$<0,開(kāi)口向下,對(duì)稱軸t=$\frac{9}{2}$,
∴3≤t<$\frac{9}{2}$時(shí),S隨t的增大而增大.
綜上所述,當(dāng)當(dāng)0<t≤1.5或3≤t<$\frac{9}{2}$時(shí),S隨t的增大而增大.
點(diǎn)評(píng) 本題考查三角形綜合題、正方形的判定和性質(zhì)、勾股定理、平行線分線段成比例定理、二次函數(shù)的應(yīng)用等知識(shí),解題的關(guān)鍵是靈活運(yùn)用所學(xué)知識(shí),學(xué)會(huì)用分類討論的思想思考問(wèn)題,學(xué)會(huì)構(gòu)建二次函數(shù),利用二次函數(shù)的性質(zhì)解決增減性問(wèn)題,屬于中考?jí)狠S題.


 時(shí)刻準(zhǔn)備著暑假作業(yè)原子能出版社系列答案
時(shí)刻準(zhǔn)備著暑假作業(yè)原子能出版社系列答案 暑假銜接教材期末暑假預(yù)習(xí)武漢出版社系列答案
暑假銜接教材期末暑假預(yù)習(xí)武漢出版社系列答案 假期作業(yè)暑假成長(zhǎng)樂(lè)園新疆青少年出版社系列答案
假期作業(yè)暑假成長(zhǎng)樂(lè)園新疆青少年出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{m}{sinα}$ | B. | mcosα | C. | msinα | D. | $\frac{m}{cosα}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
| 摸球總次數(shù) | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和為6”出現(xiàn)的頻數(shù) | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和為6”出現(xiàn)的頻數(shù) | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 120.7×109 | B. | 12.07×1010 | C. | 1.207×1011 | D. | 0.1207×1012 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 6.37×106米 | B. | 6.37×107米 | C. | 0.637×107米 | D. | 63.7×105米 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
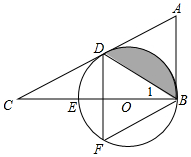 如圖,在△ABC中,∠ABC=90°,D是AC邊上一點(diǎn),連接BD,使∠A=2∠1,E是BC上的一點(diǎn),以BE為直徑的⊙O經(jīng)過(guò)點(diǎn)D,點(diǎn)F在弧DEB上.
如圖,在△ABC中,∠ABC=90°,D是AC邊上一點(diǎn),連接BD,使∠A=2∠1,E是BC上的一點(diǎn),以BE為直徑的⊙O經(jīng)過(guò)點(diǎn)D,點(diǎn)F在弧DEB上.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com