
 在△ABC中,AD⊥BC,∠B=45°,∠C=30°,CD=3.
在△ABC中,AD⊥BC,∠B=45°,∠C=30°,CD=3.分析 (1)先根據直角三角形的性質求出AD的長,再根據直角三角形的性質求出AB的長;
(2)由等腰直角三角形的性質即可得出AD=BD,可求BC,再根據三角形的面積公式可得出結論.
解答 解:(1)∵AD⊥BC,∠C=30°,CD=3,
∴AD=$\frac{\sqrt{3}}{3}$CD=$\sqrt{3}$,
∵∠B=45°,
∴AB=$\sqrt{2}$AD=$\sqrt{6}$;
(2)AD=BD=$\sqrt{3}$,
△ABC面積=($\sqrt{3}$+3)×$\sqrt{3}$÷2=$\frac{3+3\sqrt{3}}{2}$.
點評 本題考查的是勾股定理,直角三角形的性質,等腰直角三角形的性質,三角形的面積,求出AD的長是解答此題的關鍵,.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
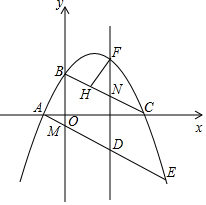 如圖所示,在平面直角坐標系中,拋物線y=ax2+bx+2(a≠0)經過點B,與x軸交于點A,C(點A在點C的左側),A(-1,0),C(4,0),連接AB,BC,點M(0,-$\frac{1}{2}$)為y軸負半軸上的一點,連接AM并延長交拋物線于點E,點D為線段AE上的一個動點,過點D作y軸的平行線與拋物線交于點F,與線段BC交于點N
如圖所示,在平面直角坐標系中,拋物線y=ax2+bx+2(a≠0)經過點B,與x軸交于點A,C(點A在點C的左側),A(-1,0),C(4,0),連接AB,BC,點M(0,-$\frac{1}{2}$)為y軸負半軸上的一點,連接AM并延長交拋物線于點E,點D為線段AE上的一個動點,過點D作y軸的平行線與拋物線交于點F,與線段BC交于點N查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,建筑物AB的高為6m,在其正東方向有一個通信塔CD,在它們之間的地面點M(B,M,D三點在一條直線上)處測得建筑物頂端A,塔頂C的仰角分別為37°和60°,在A處測得塔頂C的仰角為30°,則通信塔CD的高度.(精確到0.01m)
如圖,建筑物AB的高為6m,在其正東方向有一個通信塔CD,在它們之間的地面點M(B,M,D三點在一條直線上)處測得建筑物頂端A,塔頂C的仰角分別為37°和60°,在A處測得塔頂C的仰角為30°,則通信塔CD的高度.(精確到0.01m)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖,AB⊥BC于B,CD⊥BC于C,AB=5,BC=8,CD=3,E為線段BC上一點.求:當AE=DE時,BE的長度,并確定此時∠AED的度數.
已知:如圖,AB⊥BC于B,CD⊥BC于C,AB=5,BC=8,CD=3,E為線段BC上一點.求:當AE=DE時,BE的長度,并確定此時∠AED的度數.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 套餐 類型 | 月費 (元/月) | 套餐內包含內容 | 套餐外資費 | ||
| 國內數據流量(MB) | 國內主叫(分鐘) | 國內流量 | 國內主叫 | ||
| 套餐1 | 18 | 100 | 0 | 0.29 元/MB | 0.19 元/分鐘 |
| 套餐2 | 28 | 100 | 50 | ||
| 套餐3 | 38 | 300 | 50 | ||
| 套餐4 | 48 | 500 | 50 | ||
| A. | 套餐1 | B. | 套餐2 | C. | 套餐3 | D. | 套餐4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
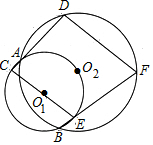 如圖,⊙O1與⊙O2經過A,B兩點,過A點的直線與⊙O1交于點C,與⊙O2交于點D,過B點的直線與⊙O1交于點E,與⊙O2交于點F.證明:CE∥DF.
如圖,⊙O1與⊙O2經過A,B兩點,過A點的直線與⊙O1交于點C,與⊙O2交于點D,過B點的直線與⊙O1交于點E,與⊙O2交于點F.證明:CE∥DF.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com