
分析 (1)利用勾股定理求出AB的長即可解決問題.
(2)如圖1中,設y=2x+b與雙曲線y=-$\frac{1}{x}$的交點為A、B.作BC⊥x軸于C,AE⊥BC于E.由AB=$\sqrt{5}$,則AE=1,BE=2,設A(m,-$\frac{1}{m}$),則B(m+1,-$\frac{1}{m}$+2),可得(m+1)(-$\frac{1}{m}$+2)=-1,解得m=$\frac{-1±\sqrt{5}}{2}$,推出A($\frac{-1-\sqrt{5}}{2}$,$\frac{\sqrt{5}-1}{2}$)或($\frac{-1+\sqrt{5}}{2}$,$\frac{-1-\sqrt{5}}{2}$),再利用待定系數法即可解決問題.
(3)如圖2中,設P(x1,y1),Q(x2,y2),由$\left\{\begin{array}{l}{y=x-2}\\{y=-{x}^{2}+mx-1}\end{array}\right.$消去y得到,x2+(m-1)x-1=0,可得x1+x2=1-m,x1x2=-1,y1=x1-2,y2=x2-2,推出y1+y2=m-5,y1y2=5-2m,
求出PQ,利用二次函數的性質,推出m=1時,非凡距離PQ的值最小,求出點P、Q的坐標,即可解決問題.
解答 解:(1)對于直線y=x+4,令x=0得y=4,令y=0得x=-4,
不妨設A(0,4),B(-4,0),
∴OA=OB=4,
∴直線l與折線AOB的非凡距離=AB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
(2)如圖1中,設y=2x+b與雙曲線y=-$\frac{1}{x}$的交點為A、B.作BC⊥x軸于C,AE⊥BC于E.
∵AB=$\sqrt{5}$,則AE=1,BE=2,設A(m,-$\frac{1}{m}$),則B(m+1,-$\frac{1}{m}$+2),
∴(m+1)(-$\frac{1}{m}$+2)=-1,
解得m=$\frac{-1±\sqrt{5}}{2}$,
∴A($\frac{-1-\sqrt{5}}{2}$,$\frac{\sqrt{5}-1}{2}$)或($\frac{-1+\sqrt{5}}{2}$,$\frac{-1-\sqrt{5}}{2}$),
把點A坐標代入y=2x+b中,可得b=$\frac{3\sqrt{5}+1}{2}$或$\frac{1-3\sqrt{5}}{2}$.
(3)如圖2中,設P(x1,y1),Q(x2,y2),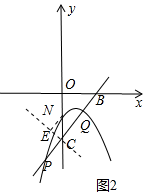
由$\left\{\begin{array}{l}{y=x-2}\\{y=-{x}^{2}+mx-1}\end{array}\right.$消去y得到,x2+(m-1)x-1=0,
∴x1+x2=1-m,x1x2=-1,y1=x1-2,y2=x2-2,
∴y1+y2=m-5,y1y2=5-2m,
∴PQ=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}+({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{(1-m)^{2}+4+(m-5)^{2}-4(5-2m)}$=$\sqrt{2(m-1)^{2}+8}$,
∵2>0,
∴m=1時,非凡距離PQ的值最小,
由$\left\{\begin{array}{l}{y=x-2}\\{y=-{x}^{2}+x-1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$,
不妨設P(-1,-3),Q(1,-1),設線段PQ與y軸的解得為C,則C(0,-2),
∴PC=CQ=$\sqrt{2}$,
∵⊙M經過P、Q兩點,
∴點M在線段PQ的中垂線EC上,作NE⊥CE于E,
∵OC=OB=2,
∴∠OCB=∠ECN=45°,
∵N(0,-1),
∴ON=1,CN=1,
在Rt△NEC中,NE=CN•cos45°=$\frac{\sqrt{2}}{2}$,
∴點N到⊙M的圓心M的距離的最小值為$\frac{\sqrt{2}}{2}$.
點評 本題考查二次函數綜合題、一次函數的應用、反比例函數的應用、一元二次方程的根與系數關系等知識,解題的關鍵是理解題意,學會利用參數解決問題,用轉化的思想思考問題,學會構建二次函數解決最值問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:選擇題
| A. | 0.296868×104 | B. | 2.96868×105 | C. | 2.96868×106 | D. | 29.6868×104 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
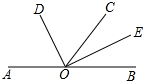 填空,完成下列說理過程:
填空,完成下列說理過程:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
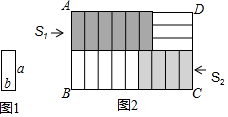 已知8個長為a,寬為b的小長方形(如圖1),不重疊無空隙地擺放(如圖2),在長方形ABCD中,AB=3b+a,當BC的長度變化時,左上角陰影面積S1與左下角陰影面積S2的差沒有變化,在a,b之間的關系應滿足( )
已知8個長為a,寬為b的小長方形(如圖1),不重疊無空隙地擺放(如圖2),在長方形ABCD中,AB=3b+a,當BC的長度變化時,左上角陰影面積S1與左下角陰影面積S2的差沒有變化,在a,b之間的關系應滿足( )| A. | 5b=2a | B. | 2b=a | C. | 3b=a | D. | 5b=3a |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2015年我市七年級學生是總體 | |
| B. | 樣本容量是1000 | |
| C. | 1000名七年級學生是總體的一個樣本 | |
| D. | 每一名七年級學生是個體 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y1>y3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com