

分析 (1)先連接AE,BP,BE,CD,構造平行四邊形AEBP,平行四邊形ADCP,進而得出四邊形BCDE是平行四邊形,即可得到DE∥BC,DE=BC,再根據CA=CB,∠ACB=90°,即可得出DE⊥AC,DE=AC;
(2)先連接AE,BP,BE,CD,構造平行四邊形AEBP,平行四邊形ADCP,進而得出四邊形BCDE是平行四邊形,即可得到DE∥BC,DE=BC,再根據Rt△ABC中,∠CAB=30°,∠ACB=90°,即可得到AC=$\sqrt{3}$BC,AC⊥BC,進而得出AC=$\sqrt{3}$DE,AC⊥DE;
(3)先連接AE,BP,BE,CD,構造平行四邊形AEBP,平行四邊形ADCP,進而得出四邊形BCDE是平行四邊形,即可得到DE∥BC,DE=BC,再根據Rt△ABC中,$\frac{BC}{AC}$=$\frac{5}{9}$,∠ACB=90°,即可得出BC=$\frac{5}{9}$AC,BC⊥AC,進而得到DE=$\frac{5}{9}$AC,DE⊥AC.
解答 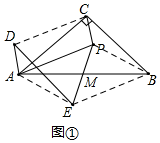 解:(1)DE∥BC,DE=BC,DE⊥AC,DE=AC.(答案不唯一)
解:(1)DE∥BC,DE=BC,DE⊥AC,DE=AC.(答案不唯一)
理由:如圖,連接AE,BP,BE,CD,
∵M分別為AB和PE的中點,
∴四邊形AEBP是平行四邊形,
∴AP∥BE,AP=BE,
又∵AD∥PC,AD=PC,
∴四邊形ADCP是平行四邊形,
∴CD=AP,CD∥AP,
∴CD=BE,CD∥BE,
∴四邊形BCDE是平行四邊形,
∴DE∥BC,DE=BC,
又∵CA=CB,∠ACB=90°,
∴DE⊥AC,DE=AC;
(2)$\sqrt{3}$DE=AC,DE⊥AC.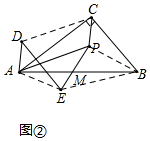
理由:如圖,連接AE,BP,BE,CD,
∵M分別為AB和PE的中點,
∴四邊形AEBP是平行四邊形,
∴AP∥BE,AP=BE,
又∵AD∥PC,AD=PC,
∴四邊形ADCP是平行四邊形,
∴CD=AP,CD∥AP,
∴CD=BE,CD∥BE,
∴四邊形BCDE是平行四邊形,
∴DE∥BC,DE=BC,
又∵在Rt△ABC中,∠CAB=30°,∠ACB=90°,
∴AC=$\sqrt{3}$BC,AC⊥BC,
∴AC=$\sqrt{3}$DE,AC⊥DE;
(3)DE=$\frac{5}{9}$AC,DE⊥AC.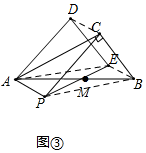
理由:如圖,連接AE,BP,BE,CD,
∵M分別為AB和PE的中點,
∴四邊形AEBP是平行四邊形,
∴AP∥BE,AP=BE,
又∵AD∥PC,AD=PC,
∴四邊形ADCP是平行四邊形,
∴CD=AP,CD∥AP,
∴CD=BE,CD∥BE,
∴四邊形BCDE是平行四邊形,
∴DE∥BC,DE=BC,
又∵在Rt△ABC中,$\frac{BC}{AC}$=$\frac{5}{9}$,∠ACB=90°,
∴BC=$\frac{5}{9}$AC,BC⊥AC,
∴DE=$\frac{5}{9}$AC,DE⊥AC.
點評 本題屬于相似形綜合題,主要考查了平行四邊形的判定與性質,等腰直角三角形的性質,含30°角的直角三角形的性質的綜合應用,解決問題的關鍵是作輔助線構造平行四邊形,依據平行四邊形的對邊平行且相等進行推導.解題時注意:在直角三角形中,30°角所對的直角邊等于斜邊的一半.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
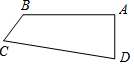 如圖,四邊形ABCD中,AB⊥AD于A,AB=8$\sqrt{6}$,AD=8$\sqrt{3}$,BC=7,CD=25,則四邊形ABCD的面積為84+96$\sqrt{2}$.
如圖,四邊形ABCD中,AB⊥AD于A,AB=8$\sqrt{6}$,AD=8$\sqrt{3}$,BC=7,CD=25,則四邊形ABCD的面積為84+96$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
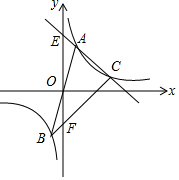 如圖,已知直線y=3x與反比例函數y=$\frac{k}{x}$的圖象交于A,B兩點,其中A(1,3),點C是反比例函數在第一象限的圖象上不同于A的一點,直線AC交y軸于點E,直線BC交y軸于點F,則線段EF的長是( )
如圖,已知直線y=3x與反比例函數y=$\frac{k}{x}$的圖象交于A,B兩點,其中A(1,3),點C是反比例函數在第一象限的圖象上不同于A的一點,直線AC交y軸于點E,直線BC交y軸于點F,則線段EF的長是( )| A. | 4 | B. | 5 | C. | 6 | D. | 變量 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
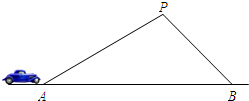 某條道路上通行車輛限速為60千米/時,在離道路50米的點P處建一個監測點,道路AB段為檢測區(如圖).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么車輛通過AB段的時間在多少秒以內時,可認定為超速(精確到0.1秒)?(參考數據:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/時=$\frac{50}{3}$米/秒)
某條道路上通行車輛限速為60千米/時,在離道路50米的點P處建一個監測點,道路AB段為檢測區(如圖).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么車輛通過AB段的時間在多少秒以內時,可認定為超速(精確到0.1秒)?(參考數據:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/時=$\frac{50}{3}$米/秒)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com