
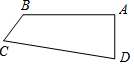
 如圖,四邊形ABCD中,AB⊥AD于A,AB=8$\sqrt{6}$,AD=8$\sqrt{3}$,BC=7,CD=25,則四邊形ABCD的面積為84+96$\sqrt{2}$.
如圖,四邊形ABCD中,AB⊥AD于A,AB=8$\sqrt{6}$,AD=8$\sqrt{3}$,BC=7,CD=25,則四邊形ABCD的面積為84+96$\sqrt{2}$. 分析 連接BD,在Rt△ABD中,已知AB,AD的長,運用勾股定理可求出BD的長,在△BCD中,已知三邊長,運用勾股定理逆定理,可得此三角形為直角三角形,故四邊形ABCD的面積為Rt△ABD與Rt△CBD的面積之和.
解答 解:連接BD,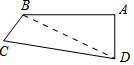
∵AB⊥AD,
∴∠A=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=24,
∵BC2+BD2=72+242=625=252=CD2,
∴△CBD為直角三角形,
∴S四邊形ABCD=S△ABD+S△BCD
=$\frac{1}{2}$×8$\sqrt{6}$×8$\sqrt{3}$+$\frac{1}{2}$×24×7
=96$\sqrt{2}$+84.
點評 本題考查的是勾股定理的逆定理及三角形的面積公式,根據題意作出輔助線,判斷出△CBD的形狀是解答此題的關鍵.


科目:初中數學 來源: 題型:填空題
 如圖,有一顆棋子放在圖中的1號位置上,現按順時針方向,第一次跳一步到2號位置上第二次跳兩步跳到4號位置上,第三次跳三步又跳到了1號位置上,第四次跳四步…一直進行下去,那么第2017次跳2017步就跳到了2號位置上.
如圖,有一顆棋子放在圖中的1號位置上,現按順時針方向,第一次跳一步到2號位置上第二次跳兩步跳到4號位置上,第三次跳三步又跳到了1號位置上,第四次跳四步…一直進行下去,那么第2017次跳2017步就跳到了2號位置上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
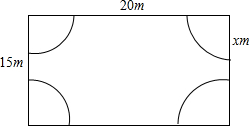 如圖所示,某小區計劃在一塊長20米,寬15米的矩形荒地上建造一個花園,使得花園所占面積為荒地面積的一半,其中花園每個角上的扇形都相同,則每個扇形的半徑x是多少?(精確到0.1)
如圖所示,某小區計劃在一塊長20米,寬15米的矩形荒地上建造一個花園,使得花園所占面積為荒地面積的一半,其中花園每個角上的扇形都相同,則每個扇形的半徑x是多少?(精確到0.1)查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com