
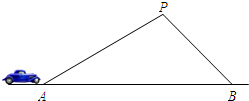
 某條道路上通行車輛限速為60千米/時,在離道路50米的點P處建一個監測點,道路AB段為檢測區(如圖).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么車輛通過AB段的時間在多少秒以內時,可認定為超速(精確到0.1秒)?(參考數據:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/時=$\frac{50}{3}$米/秒)
某條道路上通行車輛限速為60千米/時,在離道路50米的點P處建一個監測點,道路AB段為檢測區(如圖).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么車輛通過AB段的時間在多少秒以內時,可認定為超速(精確到0.1秒)?(參考數據:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/時=$\frac{50}{3}$米/秒) 分析 作PC⊥AB于點C,根據三角函數即可求得AC與BC的長,則AB即可求得,用AB的長除以速度即可求解.
解答  解:作PC⊥AB于點C.
解:作PC⊥AB于點C.
在直角△APC中,tan∠PAC=$\frac{PC}{AC}$,
則AC=$\frac{PC}{tan∠PAC}$=50$\sqrt{3}$≈86.5(米),
同理,BC=$\frac{PC}{tan∠PBA}$=PC=50(米),
則AB=AC+BC≈136.5(米),
60千米/時=$\frac{50}{3}$米/秒,
則136.5÷$\frac{50}{3}$≈8.2(秒).
故車輛通過AB段的時間在8.2秒內時,可認定為超速.
點評 本題考查解直角三角形的應用,屬于實際應用類題目,從復雜的實際問題中整理出直角三角形是解決此類問題的關鍵.


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 調查某型號節能燈泡的使用壽命 | |
| B. | 調查某品牌手機的市場占有率 | |
| C. | 調查我校初一(1)班的男女同學的比例 | |
| D. | 調查電視劇《羋月傳》在全國的收視率 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com