Question

實驗與探究：

三角點陣前n行的點數計算

如圖是一個三角點陣，從上向下數有無數多行，其中第一行有1個點，第二行有2個點…第n行有n個點…

容易發現，10是三角點陣中前4行的點數約和，你能發現300是前多少行的點數的和嗎？

如果要用試驗的方法，由上而下地逐行的相加其點數，雖然你能發現1+2+3+4+…+23+24=300．得知300是前24行的點數的和，但是這樣尋找答案需我們先探求三角點陣中前n行的點數的和與n的數量關系

前n行的點數的和是1+2+3+…+（n﹣2）+（n﹣1）+n，可以發現．

2×[1+2+3+…+（n﹣2）+（n﹣1）+n]

=[1+2+3+…+（n﹣2）+（n﹣1）+n]+[n+（n﹣1）+（n﹣2）+…3+2+1]

把兩個中括號中的第一項相加，第二項相加…第n項相加，上式等號的后邊變形為這n個小括號都等于n+1，整個式子等于n（n+1），于是得到

1+2+3+…+（n﹣2）+（n﹣1）+n=n（n+1）

這就是說，三角點陣中前n項的點數的和是n（n+1）

下列用一元二次方程解決上述問題

設三角點陣中前n行的點數的和為300，則有n（n+1）

整理這個方程，得：n2+n﹣600=0

解方程得：n1=24，n2=25

根據問題中未知數的意義確定n=24，即三角點陣中前24行的點數的和是300．

請你根據上述材料回答下列問題：

（1）三角點陣中前n行的點數的和能是600嗎？如果能，求出n；如果不能，試用一元二次方程說明道理．

（2）如果把圖中的三角點陣中各行的點數依次換成2、4、6、…、2n、…，你能探究處前n行的點數的和滿足什么規律嗎？這個三角點陣中前n行的點數的和能使600嗎？如果能，求出n；如果不能，試用一元二次方程說明道理．

 

 

Answer 1

（1）600；（2）24．

【解析】

試題分析：（1）由題意，列出方程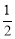n（n+1）=600，解方程得到n的值即可．

（2）根據2+4+6+…+2n=2（1+2+3+…+n）=2×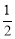n（n+1）= n（n+1），根據規律可得n（n+1）=600，求n的值即可．

試題解析：【解析】
（1）由題意可得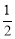：n（n+1）=600，

整理得n2+n﹣1200=0，

此方程無正整數解，

∴三角點陣中前n行的點數的和不可能是600．

（2）由題意可得：2+4+6+…+2n=2（1+2+3+…+n）=2×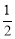n（n+1）= n（n+1），

依題意，得n（n+1）=600，

整理得n2+n﹣600=0，（n+25）（n﹣24）=0，

∴n1=﹣25，n2=24．

∵n為正整數，∴n=24．

∴n的值是24．

考點：1．探索規律題（圖形的變化類）；2．閱讀理解型問題；3．一元二次方程的應用．