
分析 根據點P在拋物線y=x2-2mx+m2+m-1上,設p點坐標為P(a,a2-2ma+m2+m-1),表示出AP2,根據二次函數的最值問題得出AP的最小值即可.
解答 解:設P點坐標為P(a,a2-2ma+m2+m-1),
AP2=(m-a)2+[a2-2ma+m2+m-1-(m+1)]2
=(m-a)2+[(m-a)2-2]2
令(m-a)2=t(t≥0)
則有AP2=t+(t-2)2=t2-3t+4=(t-$\frac{3}{2}$)2+$\frac{7}{4}$,
所以,當t=$\frac{3}{2}$ 時,AP2有最小值 $\frac{7}{4}$,
所以AP=$\frac{\sqrt{7}}{2}$,
故答案為$\frac{\sqrt{7}}{2}$.
點評 本題考查了二次函數圖象上點的坐標特征,設出點P坐標得到關于t的二次函數是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
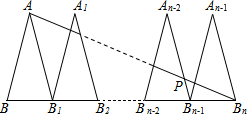 如圖,△ABB1,△A1B1B2,…,△An-2Bn-2Bn-1,△An-1Bn-1Bn是n個全等的等腰三角形,其中AB=2,BB1=1,底邊BB1,B1B2,…,Bn-2Bn-1,Bn-1Bn在同一條直線上,連接ABn交An-2Bn-1于點P,則PBn-1的值為$\frac{2}{n-1}$.
如圖,△ABB1,△A1B1B2,…,△An-2Bn-2Bn-1,△An-1Bn-1Bn是n個全等的等腰三角形,其中AB=2,BB1=1,底邊BB1,B1B2,…,Bn-2Bn-1,Bn-1Bn在同一條直線上,連接ABn交An-2Bn-1于點P,則PBn-1的值為$\frac{2}{n-1}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com