
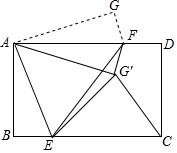
 如圖所示,矩形紙片ABCD中,AB=6,CB=8,現將紙片折疊壓平,使A,C兩點重合,折痕為EF,點D的對應點為G,再將△AGF沿著AF翻折,得△AG′F,連接EG′和CG′,則△EG′C的面積是$\frac{43}{4}$.
如圖所示,矩形紙片ABCD中,AB=6,CB=8,現將紙片折疊壓平,使A,C兩點重合,折痕為EF,點D的對應點為G,再將△AGF沿著AF翻折,得△AG′F,連接EG′和CG′,則△EG′C的面積是$\frac{43}{4}$. 分析 先連接GG'并延長,交BC于Q,則GG'⊥AD,GQ⊥BC,GH=G'H,由折疊可得,DF=GF,AG=CD=6,∠CEF=∠AEF,由AD∥BC可得,∠CEF=∠AFE,進而得出AE=CE=AF,再根據勾股定理求得AF=CE=$\frac{25}{4}$,DF=GF=$\frac{7}{4}$,在Rt△AGF中,$\frac{1}{2}$×AG×GF=$\frac{1}{2}$×AF×GH,求得GH=$\frac{64}{25}$=G'H,進而得出G'Q=6-$\frac{64}{25}$=$\frac{86}{25}$,最后計算△EG′C的面積.
解答 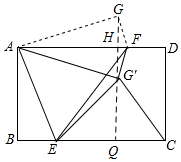 解:連接GG'并延長,交BC于Q,則GG'⊥AD,GQ⊥BC,GH=G'H,
解:連接GG'并延長,交BC于Q,則GG'⊥AD,GQ⊥BC,GH=G'H,
由折疊可得,DF=GF,AG=CD=6,∠CEF=∠AEF,
由AD∥BC可得,∠CEF=∠AFE,
∴∠AEF=∠AFE,
∴AE=CE=AF,
設AE=CE=AF=x,則DF=GF=8-x,
在Rt△AFG中,62+(8-x)2=x2,
解得x=$\frac{25}{4}$,
∴AF=CE=$\frac{25}{4}$,DF=GF=$\frac{7}{4}$,
在Rt△AGF中,$\frac{1}{2}$×AG×GF=$\frac{1}{2}$×AF×GH,
∴$\frac{1}{2}$×6×$\frac{7}{4}$=$\frac{1}{2}$×$\frac{25}{4}$×GH,
∴GH=$\frac{42}{25}$=G'H,
∴G'Q=6-$\frac{42}{25}$=$\frac{108}{25}$,
∴△EG′C的面積=$\frac{1}{2}$×G'Q×CE=$\frac{1}{2}$×$\frac{108}{25}$×$\frac{25}{4}$=$\frac{27}{2}$.
故答案為:$\frac{27}{2}$.
點評 本題屬于折疊問題,主要考查了軸對稱的性質以及矩形的性質,勾股定理的綜合應用,解決問題的關鍵是掌握:折疊是一種對稱變換,它屬于軸對稱,折疊前后圖形的形狀和大小不變,位置變化,對應邊和對應角相等.解題時注意方程思想和面積法的運用.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:選擇題
| A. | ab2的次數是2 | B. | 1是單項式 | ||
| C. | $\frac{-3{a}^{3}c}{7}$系數是-3 | D. | 多項式a+b2的次數是3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 23cm | B. | 24cm | C. | 25cm | D. | 26cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com