
 如圖,已知:△ABC中,AB=AC,M、D、E分別是BC、AB、AC的中點.
如圖,已知:△ABC中,AB=AC,M、D、E分別是BC、AB、AC的中點.分析 (1)連結(jié)AM,根據(jù)等腰三角形三線合一的性質(zhì)得到AM⊥BC,再根據(jù)直角三角形斜邊上的中線等于斜邊的一半得出MD=$\frac{1}{2}$AB,ME=$\frac{1}{2}$AC,進(jìn)而得到MD=ME;
(2)根據(jù)(1)可得AB=2MD=8,那么AC=AB=8.
解答 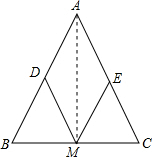 (1)證明:如圖,連結(jié)AM.
(1)證明:如圖,連結(jié)AM.
∵AB=AC,M是BC的中點,
∴AM⊥BC,
∵D、E分別是AB、AC的中點,
∴MD=$\frac{1}{2}$AB,ME=$\frac{1}{2}$AC,
∵AB=AC,
∴MD=ME;
(2)解:∵M(jìn)D=$\frac{1}{2}$AB,
∴AB=2MD=8,
∴AC=AB=8.
點評 本題考查了直角三角形斜邊上的中線的性質(zhì):在直角三角形中,斜邊上的中線等于斜邊的一半,也考查了等腰三角形三線合一的性質(zhì).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
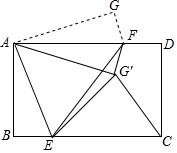 如圖所示,矩形紙片ABCD中,AB=6,CB=8,現(xiàn)將紙片折疊壓平,使A,C兩點重合,折痕為EF,點D的對應(yīng)點為G,再將△AGF沿著AF翻折,得△AG′F,連接EG′和CG′,則△EG′C的面積是$\frac{43}{4}$.
如圖所示,矩形紙片ABCD中,AB=6,CB=8,現(xiàn)將紙片折疊壓平,使A,C兩點重合,折痕為EF,點D的對應(yīng)點為G,再將△AGF沿著AF翻折,得△AG′F,連接EG′和CG′,則△EG′C的面積是$\frac{43}{4}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,OP=1,過P作PP1⊥OP,得OP1=$\sqrt{2}$;再過P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又過P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法繼續(xù)作下去,得OP2016的值等于( )
如圖,OP=1,過P作PP1⊥OP,得OP1=$\sqrt{2}$;再過P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又過P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法繼續(xù)作下去,得OP2016的值等于( )| A. | $\sqrt{2014}$ | B. | $\sqrt{2015}$ | C. | $\sqrt{2016}$ | D. | $\sqrt{2017}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
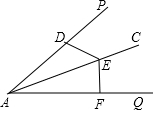 如圖,已知AC平分∠PAQ,D、E、F分別是AP、AC、AQ上的三個動點,下列說法不正確的是( )
如圖,已知AC平分∠PAQ,D、E、F分別是AP、AC、AQ上的三個動點,下列說法不正確的是( )| A. | DE⊥AP,EF⊥AQ,可推出AD=AF | B. | 若DE=EF,可推出AD=AF | ||
| C. | 若∠DEA=∠FEA,可推出AD=AF | D. | 若∠ADE=∠AFE,可推出AD=AF |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
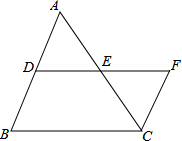 如圖,D、E是△ABC的邊AB、AC的中點,延長DE至F使EF=DE,則S△CFE:S四邊形BCFD的值為( )
如圖,D、E是△ABC的邊AB、AC的中點,延長DE至F使EF=DE,則S△CFE:S四邊形BCFD的值為( )| A. | 1:3 | B. | 2:3 | C. | 1:4 | D. | 2:5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
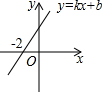 如圖,一次函數(shù)y=kx+b的圖象與x軸的交點坐標(biāo)為(-2,0),則下列說法:
如圖,一次函數(shù)y=kx+b的圖象與x軸的交點坐標(biāo)為(-2,0),則下列說法:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com