
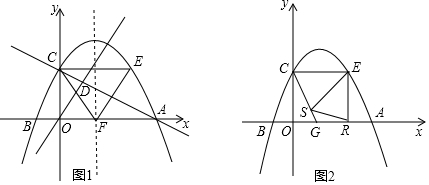
分析 (1)由拋物線y=-$\frac{1}{2}$x2+bx+c與x軸交于點A(4,0)和點B(-1,0),可知拋物線的解析式為y=-$\frac{1}{2}$(x-4)(x+1),寫成一般式即可.
(2)首先求出點D的坐標,只要證明DF平分∠CFE,CD平分∠ECF即可.
(3)①分三種情形,想辦法列出方程即可解決問題.②如圖由題意,動點B′在以C為圓心$\sqrt{5}$為半徑的⊙C上,易知當B′在線段CE上時,EB′最小.此時∠ECG=∠CGB=∠BCG,推出BC=BG,推出OG=BC-OB=$\sqrt{5}$-1.
解答 (1)解:∵拋物線y=-$\frac{1}{2}$x2+bx+c與x軸交于點A(4,0)和點B(-1,0),
∴拋物線的解析式為y=-$\frac{1}{2}$(x-4)(x+1)=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)證明:如圖1中,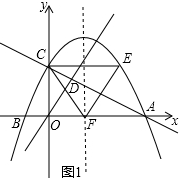
∵A(4,0),B(-1,0),C(0,2),
∴OB=1,OA=4,OC=2,
∴直線AC的解析式為y=-$\frac{1}{2}$x+2,設D(m,-$\frac{1}{2}$m+2),
∴S△ABC=$\frac{1}{2}$×5×2=5,
由題意S△AOD=$\frac{1}{2}$S△ABC,
∴$\frac{1}{2}$×4×(-$\frac{1}{2}$m+2)=$\frac{5}{2}$,
∴m=$\frac{3}{2}$,
∴D($\frac{3}{2}$,$\frac{5}{4}$),
∵拋物線的對稱軸x=$\frac{3}{2}$,
∴點D在對稱軸上,DF平分∠CFE,
在Rt△COF中,CF=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$,∵AF=$\frac{5}{2}$,
∴CF=AF,
∴∠FAC=∠FCA,
∵CE∥OA,
∴∠ECA=∠CAF=∠ACF,
∴CD平分∠ECF,
∴點D是△ECF的內心.
(3)①如圖2中,設G(m,0),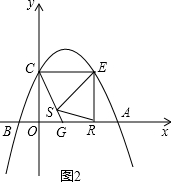
當ES=ER時,由△OCG∽△SEC,
∴$\frac{OC}{SE}$=$\frac{OG}{CS}$,
在Rt△CES中,CS=$\sqrt{C{E}^{2}-E{S}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
∴$\frac{2}{2}$=$\frac{m}{\sqrt{5}}$,
∴m=$\sqrt{5}$,
∴OG=$\sqrt{5}$.
當SE=ER時,如圖3中,作SN⊥ER于N,則EN=NR=1,S($\frac{1}{2}$m,1),SN=3-$\frac{m}{2}$,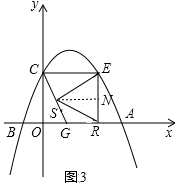
由△OCG∽△NSE,可得$\frac{OG}{EN}$=$\frac{OC}{SN}$,
∴$\frac{m}{1}$=$\frac{2}{3-\frac{m}{2}}$,
解得m=3-$\sqrt{5}$或3+$\sqrt{5}$(舍棄),
∴OG=3-$\sqrt{5}$.
當RE=RS時,如圖4中,作RN⊥SE于N,GM⊥RN于M.則SN=EN=GM,設SN=EN=GM=x,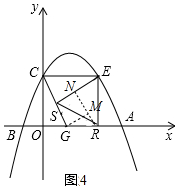
由△OCG∽△MGR,可得$\frac{CG}{GR}$=$\frac{OC}{GM}$,
∴$\frac{\sqrt{4+{m}^{2}}}{3-m}$=$\frac{2}{x}$,
∴x=$\frac{2(3-m)}{\sqrt{4+{m}^{2}}}$,
∴SN=EN=GM=$\frac{2(3-m)}{\sqrt{4+{m}^{2}}}$,
由△OCG∽△NRE,可得$\frac{OG}{EN}$=$\frac{CG}{ER}$,
∴$\frac{m}{\frac{2(3-m)}{\sqrt{4+{m}^{2}}}}$=$\frac{\sqrt{4+{m}^{2}}}{2}$,
解得m=$\frac{3}{2}$,
∴OG=$\frac{3}{2}$,
綜上所述,當△ESR是等腰三角形時,OG的長為$\sqrt{5}$或3-$\sqrt{5}$或$\frac{3}{2}$.
②如圖5中,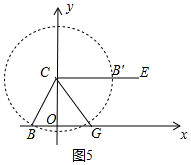
如圖由題意,動點B′在以C為圓心$\sqrt{5}$為半徑的⊙C上,易知當B′在線段CE上時,EB′最小.
此時∠ECG=∠CGB=∠BCG,
∴BC=BG,
∴OG=BC-OB=$\sqrt{5}$-1.
點評 本題考查二次函數綜合題、待定系數法、等腰三角形的判定和性質、圓的有關知識、勾股定理、三角形的內心、一元二次方程等知識,解題的關鍵是靈活運用所學知識,學會用分類討論的思想思考問題,學會利用參數,構建方程解決問題,屬于中考壓軸題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
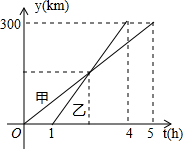 如圖,甲、乙兩車從A城出發勻速行駛至B城,在整個行駛過程中,甲、乙兩車離開A成的距離y(千米)與甲車行駛的時間t(時)之間的關系如圖所示,觀察圖象回答下列問題:
如圖,甲、乙兩車從A城出發勻速行駛至B城,在整個行駛過程中,甲、乙兩車離開A成的距離y(千米)與甲車行駛的時間t(時)之間的關系如圖所示,觀察圖象回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
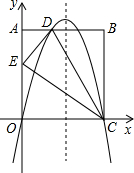 如圖,在矩形ABCD中,AO=10,AB=8,分別以OC、OA所在的直線為x軸,y軸建立平面直角坐標系,點D(3,10)、E(0,6),拋物線y=ax2+bx+c經過O,D,C三點.
如圖,在矩形ABCD中,AO=10,AB=8,分別以OC、OA所在的直線為x軸,y軸建立平面直角坐標系,點D(3,10)、E(0,6),拋物線y=ax2+bx+c經過O,D,C三點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com