
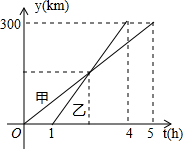
 如圖,甲、乙兩車從A城出發勻速行駛至B城,在整個行駛過程中,甲、乙兩車離開A成的距離y(千米)與甲車行駛的時間t(時)之間的關系如圖所示,觀察圖象回答下列問題:
如圖,甲、乙兩車從A城出發勻速行駛至B城,在整個行駛過程中,甲、乙兩車離開A成的距離y(千米)與甲車行駛的時間t(時)之間的關系如圖所示,觀察圖象回答下列問題:分析 (1)根據函數圖象可以直接得到A,B兩城的距離;
(2)根據函數圖象中的數據可以得到若兩車同時出發,乙車將比甲車早到幾小時;
(3)根據函數圖象中的數據可以求得乙車的速度和乙車出發幾小時兩車相遇;
(4)根據函數圖象中的數據可以分別求得甲、乙兩車對應的函數解析式,從而可以解答本題.
解答 解:(1)由圖象可得,
A,B兩城相距300千米,
故答案為:300;
(2)由圖象可得,
若兩車同時出發,乙車將比甲車早到:5-(4-1)=5-3=2(小時),
故答案為:2;
(3)由圖象可得,
乙車的速度為:300÷(4-1)=100千米/時,
設乙車出發x小時時兩車相遇,
$\frac{300}{5}×(x+1)=100x$,
解得,x=1.5,
故答案為:100,1.5;
(4)設甲車對應的函數解析式為y=kx,
5k=300,得k=60,
∴甲車對應的函數解析式為y=60x,
設乙車對應的函數解析式為y=ax+b,
$\left\{\begin{array}{l}{a+b=0}\\{4a+b=300}\end{array}\right.$,得$\left\{\begin{array}{l}{a=100}\\{b=-100}\end{array}\right.$,
即乙車對應的函數解析式為y=100x-100,
∴|(100x-100)-60x|=40,
解得,${x}_{1}=\frac{3}{2}$,${x}_{2}=\frac{7}{2}$,
當x=$\frac{3}{2}$時,乙出發$\frac{3}{2}-1=\frac{1}{2}$小時,
當x=$\frac{7}{2}$時,乙出發$\frac{7}{2}-1=\frac{5}{2}$小時,
即當乙車出發$\frac{1}{2}$小時或$\frac{5}{2}$小時時,甲、乙兩車相距40千米.
點評 本題考查一次函數的應用,解答本題的關鍵是明確題意,找出所求問題需要的條件,利用函數的性質數形結合的思想解答,注意第(4)問中求得是乙車出發幾小時,這也是易錯點,容易求出甲車出發的時間誤認為是乙車出發的時間.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com