
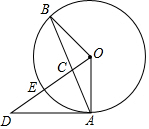
 如圖,A、B是⊙O上的兩點,過O作OB的垂線交AB于C,交⊙O于E,交⊙O的切線AD于D.
如圖,A、B是⊙O上的兩點,過O作OB的垂線交AB于C,交⊙O于E,交⊙O的切線AD于D.分析 (1)要證明DA=DC,只要證明∠ACD=∠CAD即可,根據題目中的條件可以得到∠ACD=∠CAD,結論得以證明;
(2)根據(1)中的結論和勾股定理可以求得DA及DE的長.
解答 (1)證明:∵OB⊥OC,OA⊥AD,
∴∠BOC=90°,∠OAD=90°,
∴∠BCO+∠OBC=∠OAC+∠CAD=90°,
∵OB=OA,
∴∠OBC=∠OAC,
∴∠BCO=∠CAD,
∵∠BCO=∠ACD,
∴∠ACD=∠CAD,
∴DA=DC;
(2)解:∵OA=5,OC=1,∠OAD=90°,DA=DC,
∴設DA=x,
則52+x2=(x+1)2,
解得,x=12,
∴DA=12,OD=13,
∵OE=OA,
∴OE=5,
∴DE=OD-OC=13-5=8.
點評 本題考查切線的性質,解答此類題目的關鍵是明確題目中所要證明的結論和所要解答的問題,然后根據數形結合和勾股定理的相關知識解答.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
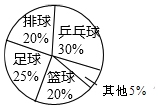 如圖是某班學生最喜歡的球類活動人數統計圖,則下列說法不正確的是( )
如圖是某班學生最喜歡的球類活動人數統計圖,則下列說法不正確的是( )| A. | 該班喜歡乒乓球的學生最多 | |
| B. | 該班喜歡排球和籃球的學生一樣多 | |
| C. | 該班喜歡足球的人數是喜歡排球人數的1.25倍 | |
| D. | 該班喜歡其他球類活動的人數為5人 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com