
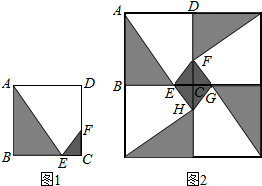
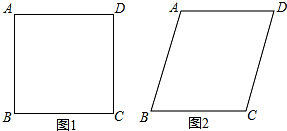
分析 (1)圖(2)可以看作是由四塊圖(1)所示地磚繞C點按順(逆)時針方向旋轉90°后得到的,故CE=CF=CG.所以△CEF是等腰直角三角形.因此四邊形EFGH是正方形.
(2)費用由三部分的費用組成,因此需求各個部分的面積.因為CE=CF,所以可設CE=x,用含x的式子表示各部分的面積,得出費用的表達式,再運用函數性質解答.
解答 解:(1)四邊形EFGH是正方形,
圖(2)可以看作是由四塊圖(1)所示地磚繞C點按順(逆)時針方向旋轉90°后得到的,
故CE=CF=CG.
∴△CEF是等腰直角三角形.
∴四邊形EFGH是正方形;
(2)設CE=x,則BE=0.4-x,每塊地磚的費用為y,
那么y=$\frac{1}{2}$x2×50+$\frac{1}{2}$×0.4×(0.4-x)×40+[0.16-$\frac{1}{2}$x2-$\frac{1}{2}$×0.4×(0.4-x)]×30
=10x2-3x+12.6
=10[(x-0.15)2+12.375(0<x<0.6).
當x=0.15時,y有最小值,即費用為最省,此時CE=CF=0.15.
答:當CE=CF=0.15米時,總費用最省.
點評 此題主要考查了一元二次方程的應用以及圖形面積求法等知識,借助數形結合得出圖形面積關系是解題關鍵.


科目:初中數學 來源:2017屆江蘇省無錫市九年級3月月考數學試卷(解析版) 題型:填空題
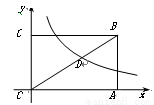
已知矩形OABC的面積為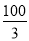 ,它的對角線OB與雙曲線
,它的對角線OB與雙曲線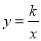 相交于點D,且OB∶OD=5∶3,則k=__________.
相交于點D,且OB∶OD=5∶3,則k=__________.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
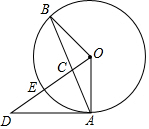 如圖,A、B是⊙O上的兩點,過O作OB的垂線交AB于C,交⊙O于E,交⊙O的切線AD于D.
如圖,A、B是⊙O上的兩點,過O作OB的垂線交AB于C,交⊙O于E,交⊙O的切線AD于D.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com