
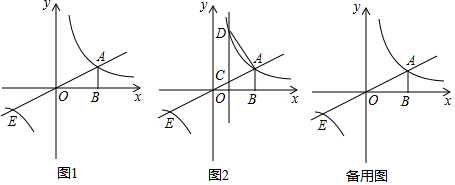
分析 (1)把A點坐標分別代入兩個函數可求得結論;
(2)根據圖象直接得出不等式k1x>$\frac{{k}_{2}}{x}$的解集;
(3)①如圖2,表示出CD=$\frac{2}{x}-\frac{1}{2}x$,PB=2-x,代入面積公式可求得S與x的函數關系式,并根據OB=2,寫出x的取值;
②分三種情況:
i)當AB為對角線時,此時CQ與AB互相垂直平分,
根據中點坐標公式得:C(1,$\frac{1}{2}$),Q(3,$\frac{1}{2}$);
ii)當AC為對角線時,此時過B作AC的垂線與AC交于點F,易得△ABF∽△AOB,由相似比可求得AF=$\frac{\sqrt{5}}{5}$,AC=$\frac{2\sqrt{5}}{5}$,由兩點之間的距離可求得C($\frac{6}{5}$,$\frac{3}{5}$),Q($\frac{6}{5}$,$\frac{8}{5}$);
iii)當BC為對角線時,則AC=1,由兩點的距離公式可求得C有兩個值,根據橫坐標不變,縱坐標減1可得此時對應的Q的坐標.
解答 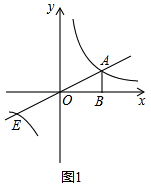 解:(1)把A(2,1)代入y=k1x中得:
解:(1)把A(2,1)代入y=k1x中得:
2k1=1,
k1=$\frac{1}{2}$,
∴直線的表達式為:y=$\frac{1}{2}$x;
把A(2,1)代入y=$\frac{{k}_{2}}{x}$中得:
1=$\frac{{k}_{2}}{2}$,k2=2,
∴雙曲線的表達式為:y=$\frac{2}{x}$;
(2)如圖1,∵點A(2,1),
∴E(-2,-1),
由圖象得不等式k1x>$\frac{{k}_{2}}{x}$的解集:-2<x<0或x>2,
故答案為:-2<x<0或x>2;
(3)①如圖2,∵P(x,0),
∴D(x,$\frac{2}{x}$),C(x,$\frac{1}{2}$x),
∴CD=$\frac{2}{x}-\frac{1}{2}x$,PB=2-x,
∴S=$\frac{1}{2}$CD•PB=$\frac{1}{2}$($\frac{2}{x}-\frac{1}{2}x$)(2-x)=$\frac{1}{4}{x}^{2}$-$\frac{1}{2}x$+$\frac{2}{x}$-1(0<x≤2);
②分三種情況:
i)如圖3,當AB為對角線時,此時CQ與AB互相垂直平分,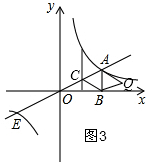
根據中點坐標公式得:C(1,$\frac{1}{2}$),Q(3,$\frac{1}{2}$);
ii)如圖4,當AC為對角線時,此時過B作AC的垂線與AC交于點F,
∵∠AFB=∠ABO=90°,∠BAF=∠BAO,
∴△ABF∽△AOB,
∴$\frac{AF}{AB}=\frac{AB}{AO}$,
∴$\frac{AF}{1}=\frac{1}{\sqrt{5}}$,
∴AF=$\frac{\sqrt{5}}{5}$,AC=2AF=$\frac{2\sqrt{5}}{5}$,
∵C(x,$\frac{1}{2}$x),A(2,1),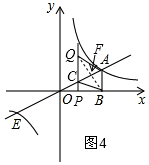
由兩點之間的距離得:AC=$\frac{2\sqrt{5}}{5}$=$\sqrt{(x-2)^{2}+(\frac{1}{2}x-1)^{2}}$,
25x2-100x+84=0
(5x-6)(5x-14)=0
x1=$\frac{6}{5}$,x2=$\frac{14}{5}$>2(舍去),
∴OP=$\frac{6}{5}$,PC=$\frac{3}{5}$,PQ=PC+CQ=$\frac{3}{5}$+1=$\frac{8}{5}$,
則C($\frac{6}{5}$,$\frac{3}{5}$),Q($\frac{6}{5}$,$\frac{8}{5}$);
iii)如圖5,當BC為對角線時,則AC=AB=1,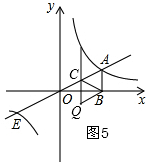
∵C(x,$\frac{1}{2}$x),A(2,1),
由兩點之間的距離得:AC=1=$\sqrt{(x-2)^{2}+(\frac{1}{2}x-1)^{2}}$,
x1=2-$\frac{2\sqrt{5}}{5}$,x2=2+$\frac{2\sqrt{5}}{5}$,
∴C1$(2-\frac{2\sqrt{5}}{5},1-\frac{\sqrt{5}}{5})$,此時對應的Q(2-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$);
C2$(2+\frac{2\sqrt{5}}{5},1+\frac{\sqrt{5}}{5})$,此時對應的Q(2+$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$);
綜上所述,點Q的坐標為:(3,$\frac{1}{2}$)或($\frac{6}{5}$,$\frac{8}{5}$)或(2-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$)或(2+$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$).
點評 本題是一次函數和反比例函數的綜合題,考查了利用待定系數法求一次函數和反比例函數的解析式、交點問題與不等式解集的關系、兩點的距離、菱形的性質和判定,采用分類討論的思想,第二問利用數形結合直接找出不等式的解集.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | “明天降雨的概率是75%”表示明天有75%的時間都在降雨 | |
| B. | “拋一枚硬幣正面朝上的概率為$\frac{1}{2}$”表示每拋2次就有1次正面朝上 | |
| C. | “拋一枚均勻的正方體骰子,朝上的點數是2的概率為$\frac{1}{6}$”表示隨著拋擲次數的增加,“拋出朝上的點數是2”這一事件發生的頻率穩定在$\frac{1}{6}$左右 | |
| D. | “彩票中獎的概率為1%”表示買100張彩票肯定會中獎 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
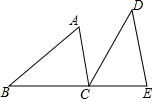 如圖,B、C、E三點在同一條直線上,AC∥DE,AC=CE,BC=DE.
如圖,B、C、E三點在同一條直線上,AC∥DE,AC=CE,BC=DE.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
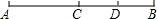 已知:如圖,點C是線段AB的中點,點D是線段BC的中點,AB=20cm,那么線段AD等于( )
已知:如圖,點C是線段AB的中點,點D是線段BC的中點,AB=20cm,那么線段AD等于( )| A. | 15cm | B. | 16cm | C. | 10cm | D. | 5cm |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com