Question

13．在平面直角坐標系xOy中，直線y=$\frac{4}{3}$x+8與x軸、y軸分別交于A，B兩點，Q是直線AB上一動點，⊙Q的半徑為1．當⊙Q與坐標軸相切時，點Q的坐標為（-$\frac{27}{4}$，-1）或（-$\frac{21}{4}$，1）或（-1，$\frac{20}{3}$）或（1，$\frac{28}{3}$）．

Answer 1

分析 畫出圖象，分四種情形討論即可．

解答 解：如圖，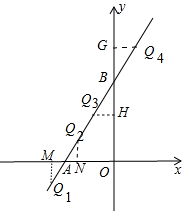

∵直線y=$\frac{4}{3}$x+8與x軸、y軸分別交于A，B兩點，
∴A（-6，0），B（0，8），
∴OA=6，OB=8，
①作Q₁M⊥x于M．當Q₁M=1時，⊙Q₁與x軸相切．
∵Q₁M∥OB，
∴$\frac{{Q}_{1}M}{OB}$=$\frac{AM}{AO}$，
∴AM=$\frac{3}{4}$，
∴Q₁（-$\frac{27}{4}$，-1）．
②作Q₂N⊥x于N．當Q₂N=1時，⊙Q₂與x軸相切，
此時Q₁，Q₂關于點A對稱，
∴Q₂（-$\frac{21}{4}$，1）．
③作Q₃H⊥y于H，當Q₃H=1時，⊙Q₃與y軸相切，
∵Q₃H∥OA，
∴$\frac{BH}{BO}$=$\frac{{Q}_{3}H}{AO}$，
∴BH=$\frac{4}{3}$，
∴OH=$\frac{20}{3}$，
∴Q₃（-1，$\frac{20}{3}$）．
④作Q₄G⊥y于G，當Q₄G=1時，⊙Q₄與y軸相切，
此時Q₃，Q₄關于點B對稱，
∴Q₄（1，$\frac{28}{3}$）．
綜上所述，滿足條件的點Q坐標為（-$\frac{27}{4}$，-1）或（-$\frac{21}{4}$，1）或（-1，$\frac{20}{3}$）或（1，$\frac{28}{3}$）．
故答案為（-$\frac{27}{4}$，-1）或（-$\frac{21}{4}$，1）或（-1，$\frac{20}{3}$）或（1，$\frac{28}{3}$）．

點評 本題考查切線的性質、一次函數的應用、平行線分線段成比例定理等知識，解題的關鍵是靈活運用所學知識解決問題，學會用分類討論的思想思考問題，注意不能漏解，屬于中考常考題型．