Question

17．如圖，在平面直角坐標系xOy中，三角板的直角頂點P的坐標為（2，2），一條直角邊與x軸的正半軸交于點A，另一直角邊與y軸交于點B，三角板繞點P在坐標平面內(nèi)轉(zhuǎn)動的過程中，當△POA為等腰三角形時，請寫出所有滿足條件的點B的坐標（0，2），（0，0），（0，4-2$\sqrt{2}$）．

Answer 1

分析 由P坐標為（2，2），可得∠AOP=45°，然后分別從OA=PA，OP=PA，OA=OP去分析求解即可求得答案．

解答 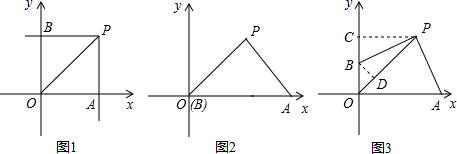解：∵P坐標為（2，2），
∴∠AOP=45°，
①如圖1，若OA=PA，則∠AOP=∠OPA=45°，
∴∠OAP=90°，
即PA⊥x軸，
∵∠APB=90°，
∴PB⊥y軸，
∴點B的坐標為：（0，2）；
②如圖2，若OP=PA，則∠AOP=∠OAP=45°，
∴∠OPA=90°，
∵∠BPA=90°，
∴點B與點O重合，
∴點B的坐標為（0，0）；
③如圖3，若OA=OP，則∠OPA=∠OAP=$\frac{180°-∠AOP}{2}$=67.5°，
過點P作PC⊥y軸于點C，過點B作BD⊥OP于點D，
則PC∥OA，
∴∠OPC=∠AOP=45°，
∵∠APB=90°，
∴∠OPB=∠APB-∠OPA=22.5°，
∴∠OPB=∠CPB=22.5°，
∴BC=BD，
設(shè)OB=a，
則BD=BC=2-a，
∵∠BOP=45°，
在Rt△OBD中，BD=OB•sin45°，
即2-a=$\frac{\sqrt{2}}{2}$a，
解得：a=4-2$\sqrt{2}$．
綜上可得：點B的坐標為：（0，2），（0，0），（0，4-2$\sqrt{2}$）．
故答案為：（0，2），（0，0），（0，4-2$\sqrt{2}$）．

點評 此題考查了等腰三角形的性質(zhì)、三角函數(shù)的定義以及旋轉(zhuǎn)的性質(zhì)．此題難度較大，注意掌握方程思想、分類討論思想以及數(shù)形結(jié)合思想的應用．