

分析 (1)根據(jù)折疊的性質(zhì)可知得到∠APO=∠B=90°,根據(jù)相似三角形的判定定理證明即可;
(2)根據(jù)勾股定理計(jì)算即可;
(3)作MH∥AB交PB于H,根據(jù)相似三角形的性質(zhì)得到BF=FH,根據(jù)等腰三角形的性質(zhì)得到PE=EH,得到答案.
解答 (1)證明:由折疊的性質(zhì)可知,∠APO=∠B=90°,
∴∠APD+∠CPO=90°,又∠APD+∠DAP=90°,
∴∠DAP=∠CPO,又∠D=∠C=90°,
∴△OCP∽△PDA;
(2)解:∵△OCP∽△PDA,面積比為1:4,
∴$\frac{CP}{AD}$=$\frac{1}{2}$,
∴CP=4,
設(shè)AB=x,則AP=x,PD=x-4,
由勾股定理得,AD2+PD2=AP2,即82+(x-4)2=x2,
解得,x=10,即AB=10;
(3)解:PB=2EF.
作MH∥AB交PB于H,
∴∠PHM=∠PBA,
∵AP=AB,
∴∠APB=∠PBA,
∴∠APB=∠PHM,
∴MP=MH,又BN=PM,
∴MH=BN,又∵M(jìn)H∥AB,
∴BF=FH,
∵M(jìn)P=MH,ME⊥BP,
∴PE=EH,
∴PB=2EF.
點(diǎn)評(píng) 本題考查的是相似三角形的判定和性質(zhì),掌握相似三角形的判定定理和性質(zhì)定理、相似三角形的面積比等于相似比的平方、翻轉(zhuǎn)變換的性質(zhì)是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | -8 | D. | 8 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
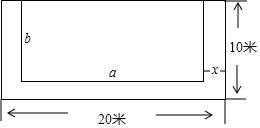 如圖,有一塊長(zhǎng)為20米,寬10米的長(zhǎng)方形土地,現(xiàn)將其余三面留出寬都是x米的小路,中間余下的長(zhǎng)方形部分做菜地,用代數(shù)式表示:
如圖,有一塊長(zhǎng)為20米,寬10米的長(zhǎng)方形土地,現(xiàn)將其余三面留出寬都是x米的小路,中間余下的長(zhǎng)方形部分做菜地,用代數(shù)式表示:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com