
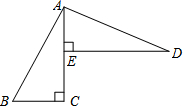
 已知:如圖,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.
已知:如圖,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.分析 (1)先根據余角的定義得出∠B=∠DAE,再由ASA定理得出△ADE≌△BAC,根據全等三角形的性質即可得出結論;
(2)根據(1)中△ADE≌△BAC可得出結論.
解答 解:(1)∵AC⊥BC,DE⊥AC,
∴∠AED=∠ACB=90°,∠B+∠BAC=90°.
∵AD⊥AB,
∴∠BAC+∠DAE=90°,
∴∠B=∠DAE.
在△ADE與△BAC中,
∵$\left\{\begin{array}{l}{∠B=∠DAE}\\{BC=AE}\\{∠ACB=∠AED}\end{array}\right.$,
∴△ADE≌△BAC(ASA),
∴AD=AB=5;
(2)BC+CE=DE.
∵由(1)知△ADE≌△BAC,
∴AC=DE,AE=BC,
∴BC+CE=DE.
點評 本題考查的是全等三角形的判定與性質,熟知全等三角形的判定定理是解答此題的關鍵.


科目:初中數學 來源: 題型:填空題
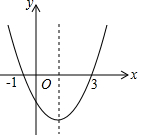 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列6個結論正確的有5個
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列6個結論正確的有5個查看答案和解析>>
科目:初中數學 來源: 題型:填空題
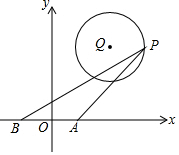 如圖,在平面直角坐標系中,Q(3,4),P是在以Q為圓心,2為半徑的⊙Q上一動點,A(1,0)、B(-1,0),連接PA、PB,則PA2+PB2的最小值是20.
如圖,在平面直角坐標系中,Q(3,4),P是在以Q為圓心,2為半徑的⊙Q上一動點,A(1,0)、B(-1,0),連接PA、PB,則PA2+PB2的最小值是20.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,△ABC中,AB=2,AC=3,1<BC<5,分別以AB、BC、AC為邊向外作正方形ABIH、BCDE和正方形ACFG,則圖中陰影部分的最大面積為( )
如圖,△ABC中,AB=2,AC=3,1<BC<5,分別以AB、BC、AC為邊向外作正方形ABIH、BCDE和正方形ACFG,則圖中陰影部分的最大面積為( )| A. | 6 | B. | 9 | C. | 11 | D. | 無法計算 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
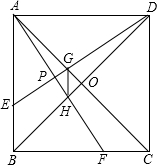 如圖,已知在正方形ABCD中,AC與BD交與點O,E、F分別是AB、BC上的點,當點E、F在相同的時間、以相同的速度分別在AB、BC上從點A向B和從點B向C方向移動,是判斷在E、F移動的期間:
如圖,已知在正方形ABCD中,AC與BD交與點O,E、F分別是AB、BC上的點,當點E、F在相同的時間、以相同的速度分別在AB、BC上從點A向B和從點B向C方向移動,是判斷在E、F移動的期間:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com