
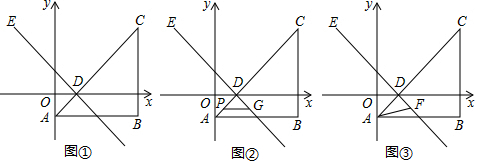
分析 (1)根據坐標的定義結合題意可得B、D、E的坐標,利用待定系數法即可求出直線DE的解析式.
(2)分兩種情形①當$0≤t≤\sqrt{2}$時,PD=$\sqrt{2}$-t,可得S=$\frac{1}{2}$PD2=$\frac{1}{2}$($\sqrt{2}$-t)2=$\frac{1}{2}$t2-$\sqrt{2}$t+1.②當$\sqrt{2}<t≤4\sqrt{2}$時,同法可求.
(3)過點E作EK∥x軸交y軸于H,則∠KEF=∠EDO=45°.過點F作FG⊥EK于點G,則FG=EG=$\frac{\sqrt{2}}{2}$EF,由題意,動點M運動的路徑為折線AF+EF,運動時間:t=AF+$\frac{\sqrt{2}}{2}$EF,推出t=AF+FG,即運動時間等于折線AF+FG的長度,由垂線段最短可知,折線AF+FG的長度的最小值為EK與線段AB之間的垂線段.則t最小=AH,直線DE與y軸的交點即為所求之F點.
解答 解:(1)如圖①中,由題意得:B(4,-1),D(1,0).E(-2,3).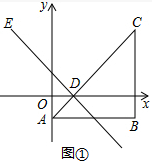
設直線DE為y=kx+b(k≠0)
把D(1,0).E(-2,3)代入得$\left\{{\begin{array}{l}{0=k+b}\\{3=-2k+b}\end{array}}\right.$
解之得:$\left\{{\begin{array}{l}{k=-1}\\{b=1}\end{array}}\right.$
∴直線DE為:y=-x+1.
(2)在Rt△ABC中,由BA=BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=4$\sqrt{2}$,
由AP=t (0≤t≤4$\sqrt{2}$),
同理可得:AD=$\sqrt{A{O}^{2}+O{D}^{2}}$=$\sqrt{2}$,
由題意可知:ED⊥AC,∠DPG=∠DAB=45°
∴△DPG為等腰直角三角形
S=$\frac{1}{2}$DP2,
如圖②中,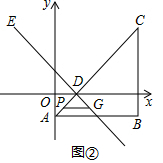
①當$0≤t≤\sqrt{2}$時,PD=$\sqrt{2}$-t,
∴S=$\frac{1}{2}$PD2=$\frac{1}{2}$($\sqrt{2}$-t)2=$\frac{1}{2}$t2-$\sqrt{2}$t+1.
②當$\sqrt{2}<t≤4\sqrt{2}$時,易得DP=t-$\sqrt{2}$,
∴S=$\frac{1}{2}$PD2=$\frac{1}{2}$(t-$\sqrt{2}$)2=$\frac{1}{2}$t2-$\sqrt{2}$t+1.
綜上:S=$\frac{1}{2}$t2-$\sqrt{2}$t+1.(0≤t$≤4\sqrt{2}$)
(3)如圖③,易得∠EDO=45°.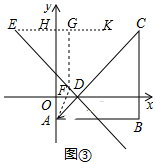
過點E作EK∥x軸交y軸于H,則∠KEF=∠EDO=45°.
過點F作FG⊥EK于點G,則FG=EG=$\frac{\sqrt{2}}{2}$EF,
由題意,動點M運動的路徑為折線AF+EF,運動時間:t=AF+$\frac{\sqrt{2}}{2}$EF,
∴t=AF+FG,即運動時間等于折線AF+FG的長度,
由垂線段最短可知,折線AF+FG的長度的最小值為EK與線段AB之間的垂線段.
則t最小=AH,直線DE與y軸的交點即為所求之F點,
∵直線DE解析式為:y=-x+1
∴F(0,1),
綜上所述,當點F(0,1)坐標為時,點M在整個運動過程中用時最少.
點評 本題考查一次函數綜合題、等腰直角三角形的性質、待定系數法、三角形的面積、垂線段最短等知識,解題的關鍵是靈活運用所學知識解決問題,學會用轉化的思想思考問題,屬于中考壓軸題.


 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | -|-2|=2 | B. | (6.4×106)÷(8×103)=800 | ||
| C. | (-1)2015-12016=-2 | D. | $-6÷({\frac{1}{3}-\frac{1}{2}})=36$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
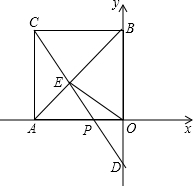 在平面直角坐標系xOy中,四邊形OACB是正方形,A點的坐標為(-3,0),點P是射線AO上(異于點A、O)一動點,直線CP與對角線AB及y軸分別交于點E,D.
在平面直角坐標系xOy中,四邊形OACB是正方形,A點的坐標為(-3,0),點P是射線AO上(異于點A、O)一動點,直線CP與對角線AB及y軸分別交于點E,D.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 為測量塔的高度,如圖,一人先在附近一樓房的底端A點處觀測觀光塔頂端C處的仰角是45°,然后爬到該樓房頂端B點處觀測觀光塔底部D處的俯角是30°.已知樓房高AB約是40m,根據以上觀測數據,求觀光塔CD的高度.
為測量塔的高度,如圖,一人先在附近一樓房的底端A點處觀測觀光塔頂端C處的仰角是45°,然后爬到該樓房頂端B點處觀測觀光塔底部D處的俯角是30°.已知樓房高AB約是40m,根據以上觀測數據,求觀光塔CD的高度.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com