
 如圖,在四邊形ABCD中,∠D=90°,AB=12,CD=3,DA=4,BC=13,求S四邊形ABCD.
如圖,在四邊形ABCD中,∠D=90°,AB=12,CD=3,DA=4,BC=13,求S四邊形ABCD. 分析 先連接AC,在△ADC中利用勾股定理求出AC的長,再根據勾股定理的逆定理判斷出△ABC是直角三角形,再根據S四邊形ABCD=S△ACD+S△ACB進行解答即可.
解答 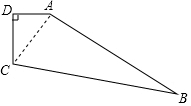 解:連接AC.
解:連接AC.
在△ADC中,
∵∠D=90°,
∴AC2=AD2+CD2(勾股定理).
由CD=3,AD=4,
得AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=5,
在△ABC中,
∵AB=12,BC=13,
∴BC2-AB2=132-122=25,
得:BC2=AB2+AC2,
∴∠CAB=90°(勾股定理的逆定理).
因此,S四邊形ABCD=S△ACD+S△ACB
=$\frac{1}{2}$AD•DC+$\frac{1}{2}$AB•AC
=$\frac{1}{2}$×4×3+$\frac{1}{2}$×12×5
=6+30
=36.
點評 本題考查的是勾股定理及其逆定理,三角形的面積公式,根據勾股定理的逆定理判斷出△ABC是直角三角形是解答此題的關鍵.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2.88×102 | B. | 28.8×103 | C. | 2.88×104 | D. | 0.288×105 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如果身邊沒有質地均勻的硬幣,下列方法可以模擬擲硬幣實驗的是( )
如果身邊沒有質地均勻的硬幣,下列方法可以模擬擲硬幣實驗的是( )| A. | 擲一個瓶蓋,蓋面朝上代表正面,蓋面朝下代表反面 | |
| B. | 擲一枚圖釘,釘尖著地代表正面,釘帽著地代表反面 | |
| C. | 擲一枚質地均勻的骰子,奇數點朝上代表正面,偶數點朝上代表反面 | |
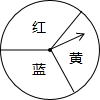
| D. | 轉動如圖所示的轉盤,指針指向“紅”代表正面,指針指向“藍”代表反面 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com