
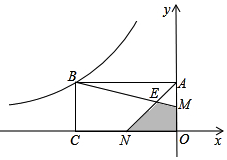
 如圖,矩形OABC的兩邊OA、OC在坐標(biāo)軸上,且OC=2OA,M、N分別為OA、OC的中點(diǎn),BM與AN交于點(diǎn)E,若四邊形EMON的面積為2,則經(jīng)過點(diǎn)B的雙曲線的解析式為( )
如圖,矩形OABC的兩邊OA、OC在坐標(biāo)軸上,且OC=2OA,M、N分別為OA、OC的中點(diǎn),BM與AN交于點(diǎn)E,若四邊形EMON的面積為2,則經(jīng)過點(diǎn)B的雙曲線的解析式為( )| A. | y=-$\frac{10}{x}$ | B. | y=-$\frac{8}{x}$ | C. | y=-$\frac{6}{x}$ | D. | y=-$\frac{4}{x}$ |
分析 過M作MG∥ON,交AN于G,過E作EF⊥AB于F,由題意可知:AM=OM=a,ON=NC=2a,AB=OC=4a,BC=AO=2a,再根據(jù)三角形相似以及三角形面積之間的關(guān)系求出B點(diǎn)坐標(biāo),即雙曲線解析式求出.
解答 解:過M作MG∥ON,交AN于G,過E作EF⊥AB于F,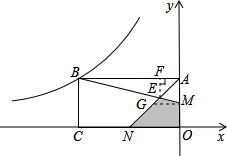
設(shè)EF=h,OM=a,
由題意可知:AM=OM=a,ON=NC=2a,AB=OC=4a,BC=AO=2a
△AON中,MG∥ON,AM=OM,
∴MG=$\frac{1}{2}$ON=a,
∵M(jìn)G∥AB
∴$\frac{MG}{AB}$=$\frac{ME}{BE}$=$\frac{1}{4}$,
∴BE=4EM,
∵EF⊥AB,
∴EF∥AM,
∴$\frac{FE}{AM}$=$\frac{BE}{BM}$=$\frac{4}{5}$.
∴FE=$\frac{4}{5}$AM,即h=$\frac{4}{5}$a,
∵S△ABM=4a×a÷2=2a2,
S△AON=2a×2a÷2=2a2,
∴S△ABM=S△AON,
∴S△AEB=S四邊形EMON=2,
S△AEB=AB×EF÷2=4a×h÷2=2,
ah=1,又有h=$\frac{4}{5}$a,a=$\frac{\sqrt{5}}{2}$(長度為正數(shù))
∴OA=$\sqrt{5}$,OC=2$\sqrt{5}$,
因此B的坐標(biāo)為(-2$\sqrt{5}$,$\sqrt{5}$),
經(jīng)過B的雙曲線的解析式就是y=-$\frac{10}{x}$.
點(diǎn)評(píng) 本題主要考查反比例函數(shù)的綜合題的知識(shí),解答本題的關(guān)鍵是輔助線的作法和相似三角形的性質(zhì)的應(yīng)用,此題難度中等.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 240人 | B. | 360人 | C. | 380人 | D. | 420人 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 8x9÷4x3=2x6 | B. | 4a2b3÷4a2b3=0 | C. | a2m÷am=a2 | D. | 2a2b÷(-$\frac{1}{2}$ab2)=-4c |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
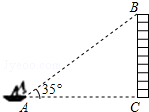 如圖,從一艘船的點(diǎn)A處觀測海岸上高為41m的燈塔BC(觀測點(diǎn)A與燈塔底部C在一個(gè)水平面上),測得燈塔頂部B的仰角為35°,則觀測點(diǎn)A到燈塔BC的距離為59m.(精確到1m)
如圖,從一艘船的點(diǎn)A處觀測海岸上高為41m的燈塔BC(觀測點(diǎn)A與燈塔底部C在一個(gè)水平面上),測得燈塔頂部B的仰角為35°,則觀測點(diǎn)A到燈塔BC的距離為59m.(精確到1m)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 三次多項(xiàng)式 | B. | 六次多項(xiàng)式 | ||
| C. | 次數(shù)不低于3的整式 | D. | 次數(shù)不高于3的整式 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com