
分析 (1)調配后企業生產A種產品的年利潤=生產A種產品的人數×原來平均每人每年可創造利潤×(1+20%);生產B種產品的年利潤=生產B種產品的人數×1.54m;總利潤=調配后企業生產A種產品的年利潤+生產B種產品的年利潤,把相關數值代入即可;
(2)關系式為:調配后企業生產A種產品的年利潤≥調配前企業年利潤的五分之四,生產B種產品的年利潤>調配前企業年利潤的一半,把相關數值代入求得x的取值范圍,根據x的實際意義確定其具體值,從而得出調配方案;再根據(1)中y與x的關系式,運用一次函數的性質,可求得利潤最大的調配方案.
解答 解:(1)生產A種產品的人數為300-x,平均每人每年創造的利潤為m×(1+20%)萬元,所以調配后企業生產A種產品的年利潤為1.2(300-x)m萬元;
生產B種產品的人數為x,平均每人每年創造的利潤為1.54m,所以生產B種產品的年利潤為1.54mx萬元;
調配后企業全年的總利潤y=1.2(300-x)m+1.54mx=360m+0.34mx.
故答案為:1.2(300-x)m;1.54mx;y=360m+0.34mx;
(2)$\left\{\begin{array}{l}{1.2(300-x)m≥\frac{4}{5}×300m}\\{1.54xm>\frac{1}{2}×300m}\end{array}\right.$,
解得:97 $\frac{31}{77}$<x≤100,
∵x為正整數,
∴x可取98,99,100.
∴共有三種調配方案:
①202人生產A種產品,98人生產B種產品;
②201人生產A種產品,99人生產B種產品;
③200人生產A種產品,100人生產B種產品;
∵y=0.34mx+360m,
∴x越大,利潤y越大,
∴當x取最大值100,即200人生產A種產品,100人生產B種產品時總利潤最大.
點評 本題考查一元一次不等式組的應用,一次函數的性質及方案選擇問題,根據關鍵語句得到相應的關系式是解決問題的關鍵.


 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:初中數學 來源: 題型:選擇題
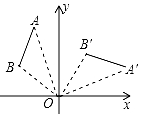 如圖,將線段AB繞點O順時針旋轉90°得到線段A′B′,那么A(-2,5)的對應點A′的坐標是( )
如圖,將線段AB繞點O順時針旋轉90°得到線段A′B′,那么A(-2,5)的對應點A′的坐標是( )| A. | (5,2) | B. | (2,5) | C. | (2,-5) | D. | (5,-2) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
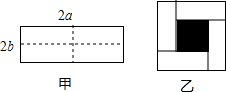
 如圖,已知等腰直角△ABC的直角邊長與正方形DEFG的邊長均為8cm,EF與AC在同一條直線上,開始時點A與點F重合,讓△ABC向左移動,運動速度為1cm/s,最后點A與點E重合.
如圖,已知等腰直角△ABC的直角邊長與正方形DEFG的邊長均為8cm,EF與AC在同一條直線上,開始時點A與點F重合,讓△ABC向左移動,運動速度為1cm/s,最后點A與點E重合.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
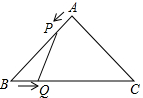 如圖,在△ABC中,AB=AC=4cm,∠BAC=90°.動點P、Q同時從A、B兩點出發,分別沿AB、BC方向勻速移動,它們的速度都是1cm/s,當點P到達點B時,P、Q兩點停止運動.設點P的運動時間為t s,四邊形APQC的面積為y cm2.
如圖,在△ABC中,AB=AC=4cm,∠BAC=90°.動點P、Q同時從A、B兩點出發,分別沿AB、BC方向勻速移動,它們的速度都是1cm/s,當點P到達點B時,P、Q兩點停止運動.設點P的運動時間為t s,四邊形APQC的面積為y cm2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,AO=BO=2,∠AOB=90°,△A′、C、D分別與點A重合,在邊BO上、在邊BO的延長線上,且A′C=A′D=$\sqrt{5}$,將△A′CD沿射線OB平移,設平移距離為x(其中0<x<3),平移后的圖形與△ABO重疊部分的面積為S.
如圖,AO=BO=2,∠AOB=90°,△A′、C、D分別與點A重合,在邊BO上、在邊BO的延長線上,且A′C=A′D=$\sqrt{5}$,將△A′CD沿射線OB平移,設平移距離為x(其中0<x<3),平移后的圖形與△ABO重疊部分的面積為S.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
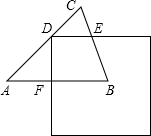 如圖,在△ABC中,AB=AC=1,∠A=60°,邊長為1的正方形的一個頂點D在邊AC上,與△ABC另兩邊分別交于點E、F,DE∥AB,將正方形平移,使點D保持在AC上(D不與A重合),設AF=x,正方形與△ABC重疊部分的面積為y.
如圖,在△ABC中,AB=AC=1,∠A=60°,邊長為1的正方形的一個頂點D在邊AC上,與△ABC另兩邊分別交于點E、F,DE∥AB,將正方形平移,使點D保持在AC上(D不與A重合),設AF=x,正方形與△ABC重疊部分的面積為y.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com