
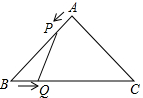
 如圖,在△ABC中,AB=AC=4cm,∠BAC=90°.動點P、Q同時從A、B兩點出發,分別沿AB、BC方向勻速移動,它們的速度都是1cm/s,當點P到達點B時,P、Q兩點停止運動.設點P的運動時間為t s,四邊形APQC的面積為y cm2.
如圖,在△ABC中,AB=AC=4cm,∠BAC=90°.動點P、Q同時從A、B兩點出發,分別沿AB、BC方向勻速移動,它們的速度都是1cm/s,當點P到達點B時,P、Q兩點停止運動.設點P的運動時間為t s,四邊形APQC的面積為y cm2.分析 (1)過P作PH⊥BC,垂足為H,解等腰直角三角形PHB,求出PH的長,利用路程=速度×時間表示出BQ,得出S△BPQ=$\frac{1}{2}$BQ•PH=$\frac{1}{2}$•t•$\frac{\sqrt{2}}{2}$(4-t)=-$\frac{\sqrt{2}}{4}$t2+$\sqrt{2}$t,那么y=S△ABC-S△BPQ,代入即可,進而根據條件得到t的取值范圍;
(2)利用配方法將(1)中所求解析式變形為頂點式,即可解決問題.
解答 解:(1)過P作PH⊥BC,垂足為H,如圖,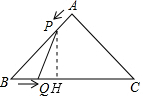 在Rt△PHB中,∵PB=AB-AP=4-t,∠B=45°,∠PHB=90°,
在Rt△PHB中,∵PB=AB-AP=4-t,∠B=45°,∠PHB=90°,
∴PH=$\frac{\sqrt{2}}{2}$PB=$\frac{\sqrt{2}}{2}$(4-t).
∴S△BPQ=$\frac{1}{2}$BQ•PH=$\frac{1}{2}$•t•$\frac{\sqrt{2}}{2}$(4-t)=-$\frac{\sqrt{2}}{4}$t2+$\sqrt{2}$t,
∴y=S△ABC-S△BPQ=$\frac{1}{2}$×4×4-(-$\frac{\sqrt{2}}{4}$t2+$\sqrt{2}$t)=$\frac{\sqrt{2}}{4}$t2-$\sqrt{2}$t+8.
∵動點P、Q同時從A、B兩點出發,分別沿AB、BC方向勻速移動,它們的速度都是1cm/s,當點P到達點B時,P、Q兩點停止運動,
∴0<t<4.
∴y與t的函數關系式為y=$\frac{\sqrt{2}}{4}$t2-$\sqrt{2}$t+8,0<t<4;
(2)y=$\frac{\sqrt{2}}{4}$t2-$\sqrt{2}$t+8=$\frac{\sqrt{2}}{4}$(t-2)2+8-$\sqrt{2}$,
∵$\frac{\sqrt{2}}{4}$>0,
∴當t=2時,y取得最小值,最小值是8-$\sqrt{2}$.
點評 本題考查了二次函數的應用,等腰直角三角形的性質,三角形的面積,求出y與t的函數關系式是解決該題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
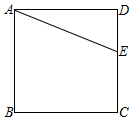 如圖,點E是正方形ABCD的邊CD上一點,把線段AE沿EC方向平移,使得點E與點C重合,得到線段CF.
如圖,點E是正方形ABCD的邊CD上一點,把線段AE沿EC方向平移,使得點E與點C重合,得到線段CF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
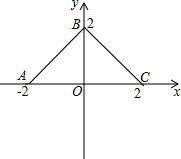 如圖,在直角坐標系上有折線段ABC,它們的坐標分別是A(-2,0),B(0,2),C(2,0),若有動直線l:y=t(0<t<2)線段AB交于M,與線段BC交于N,如果記三角形MNO的面積為S.
如圖,在直角坐標系上有折線段ABC,它們的坐標分別是A(-2,0),B(0,2),C(2,0),若有動直線l:y=t(0<t<2)線段AB交于M,與線段BC交于N,如果記三角形MNO的面積為S.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
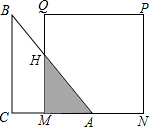 如圖,已知等腰直角三角形ABC的直角邊長與正方形MNPQ的邊長均為20cm,AC與MN在同一條直線上,開始時點A與點N重合,讓△ABC以2cm/s的速度向左運動,最終點A與點M重合.求:
如圖,已知等腰直角三角形ABC的直角邊長與正方形MNPQ的邊長均為20cm,AC與MN在同一條直線上,開始時點A與點N重合,讓△ABC以2cm/s的速度向左運動,最終點A與點M重合.求:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
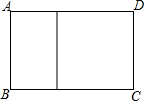 如圖,用長120cm的木條制成如圖形狀的矩形框(矩形框中間有一橫檔).設矩形框的寬AB為x(cm),所圍成的面積為S(cm2).
如圖,用長120cm的木條制成如圖形狀的矩形框(矩形框中間有一橫檔).設矩形框的寬AB為x(cm),所圍成的面積為S(cm2).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com