
 如圖,AO=BO=2,∠AOB=90°,△A′、C、D分別與點A重合,在邊BO上、在邊BO的延長線上,且A′C=A′D=$\sqrt{5}$,將△A′CD沿射線OB平移,設平移距離為x(其中0<x<3),平移后的圖形與△ABO重疊部分的面積為S.
如圖,AO=BO=2,∠AOB=90°,△A′、C、D分別與點A重合,在邊BO上、在邊BO的延長線上,且A′C=A′D=$\sqrt{5}$,將△A′CD沿射線OB平移,設平移距離為x(其中0<x<3),平移后的圖形與△ABO重疊部分的面積為S.分析 (1)勾股定理求出OD,再根據正切函數定義可得;
(2)分0<x≤1和1<x<3兩種情況,當0<x≤1時,設A′C與AB相交于點P,作PQ⊥BO于點Q,設A′D與AB相交于點M,與AO相交于點N,作MR⊥AO于點R,設PQ=h,MR=h′,解直角三角形分別得出CQ=$\frac{1}{2}$h、AR=h′、RN=MRtan∠RMN=h′tan(90°-∠MNR)=h′tan(90°-∠DNO)=h′tanD=2h′,由PQ=BQtanB=BQ即h=(1-x)+$\frac{1}{2}$h,得h=2(1-x),AN=AO-ON=2-ODtanD=2-2(1-x)=2x及AR+RN=AN得h′=$\frac{2}{3}$x,最后根據S=S△ABO-S△PBC-S△AMN可得函數解析式;當1<x<3時,設A′D與AB相交于點P,作PQ⊥BO于點Q,同理得BQ=PQ即3-x=h+$\frac{1}{2}$h,得h=$\frac{2}{3}$(3-x),根據三角形面積公式可得此時函數解析式.
解答 解:(1)如圖1,
∵∠AOB=90°,
∴OD=$\sqrt{A{D}^{2}-A{O}^{2}}$=$\sqrt{5-{2}^{2}}$=1,
∴tanD=$\frac{AO}{OD}$=$\frac{2}{1}$=2;
(2)如圖1,同理,OC=1,tan∠A′CD=2,tan∠BAO=tanB=1,
當0<x≤1時,如圖2,
設A′C與AB相交于點P,作PQ⊥BO于點Q,設A′D與AB相交于點M,與AO相交于點N,作MR⊥AO于點R,
設PQ=h,MR=h′,
在Rt△PCQ中,PQ=CQtan∠PCQ,得CQ=$\frac{1}{2}$h,
在Rt△PBQ中,PQ=BQtanB=BQ,即h=(1-x)+$\frac{1}{2}$h,得h=2(1-x),
在Rt△AMR中,MR=ARtan∠BAO=AR,即AR=h′,
在Rt△MNR中,RN=MRtan∠RMN=h′tan(90°-∠MNR)=h′tan(90°-∠DNO)=h′tanD=2h′,
∵AN=AO-ON=2-ODtanD=2-2(1-x)=2x,
AR+RN=AN,即h′+2h′=2x,得h′=$\frac{2}{3}$x,
∴S=S△ABO-S△PBC-S△AMN
=$\frac{1}{2}$AO×BO-$\frac{1}{2}$BC×PQ-$\frac{1}{2}$AN×MR
=$\frac{1}{2}$×2×2-$\frac{1}{2}$×(1-x)×2(1-x)-$\frac{1}{2}$×2x×$\frac{2}{3}$x
=-$\frac{5}{3}$x2+2x+1;
當1<x<3時,如圖3,設A′D與AB相交于點P,作PQ⊥BO于點Q,
設PQ=h,同理得BQ=PQ,
∴3-x=h+$\frac{1}{2}$h,
得h=$\frac{2}{3}$(3-x),
∴S=$\left\{\begin{array}{l}{-\frac{5}{3}{x}^{2}+2x+1}&{(0<x≤1)}\\{\frac{1}{3}{x}^{2}-2x+3}&{(1<x<3)}\end{array}\right.$.
點評 本題主要考查二次函數的應用,熟練掌握解直角三角形和解方程的能力求出所需線段的長度及割補法求三角形的面積是解題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:選擇題
| A. | 16000元 | B. | 18000元 | C. | 20000元 | D. | 22000元 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
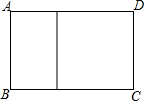 如圖,用長120cm的木條制成如圖形狀的矩形框(矩形框中間有一橫檔).設矩形框的寬AB為x(cm),所圍成的面積為S(cm2).
如圖,用長120cm的木條制成如圖形狀的矩形框(矩形框中間有一橫檔).設矩形框的寬AB為x(cm),所圍成的面積為S(cm2).查看答案和解析>>
科目:初中數學 來源: 題型:解答題

| 正方形ABCD內點的個數 | 1 | 2 | 3 | 4 | … |
| 分割成的三角形的個數 | 4 | 6 | 8 | 10 | … |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com