
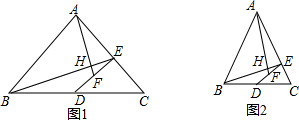
分析 連接AD,根據等腰三角形的性質可得∠ABC=∠C,∠BAD=$\frac{1}{2}$∠BAC,AD⊥BC,然后根據同角的余角相等可得∠ADE=∠C.易證△ADB∽△DEC,可得AD•CE=BD•DE.由此可得AD•CE=$\frac{1}{2}$BC•2DF=BC•DF,即$\frac{AD}{DF}=\frac{DE}{CE}$,由此可證到△AFD∽△BEC,則有$\frac{AF}{BE}=\frac{AD}{BC}$,在Rt△ADB中根據三角函數的定義可得tan∠ABD=tan(90°-$\frac{1}{2}$∠BAC)=$\frac{AD}{BD}$=$\frac{2AD}{BC}$,從而可得$\frac{AF}{BE}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上結論即可解決題中的兩個問題.
解答 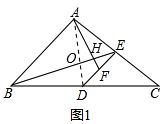 解:如圖1,連接AD,
解:如圖1,連接AD,
∵AB=AC,點D是BC的中點,
∴∠ABC=∠C,∠BAD=∠DAC=$\frac{1}{2}$∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,
∴$\frac{AD}{BD}=\frac{DE}{CE}$,
即AD•CE=BD•DE.
∵點D是BC的中點,點F是DE的中點,
∴BD=$\frac{1}{2}$BC,DE=2DF,
∴AD•CE═$\frac{1}{2}$BC•2DF=BC•DF,
∴$\frac{AD}{DF}=\frac{DE}{CE}$,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴$\frac{AF}{BE}=\frac{AD}{BC}$,
在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°-$\frac{1}{2}$∠BAC,BD=$\frac{1}{2}$BC,
∴tan∠ABD=tan(90°-$\frac{1}{2}$∠BAC)=$\frac{AD}{BD}$=$\frac{2AD}{BC}$,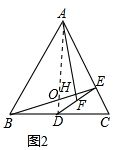
∴$\frac{AF}{BE}=\frac{AD}{BC}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°,
(1)如圖1,
根據以上結論可得:
∠AHB=90°,$\frac{AF}{BE}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$×90°)=$\frac{1}{2}$;
∴AF⊥BE,$\frac{AF}{BE}$=$\frac{1}{2}$;
(2)如圖2,
根據以上結論可得:∠AHB=90°,$\frac{AF}{BE}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$α);
∴AF⊥BE,$\frac{AF}{BE}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$α).
點評 本題主要考查的是相似三角形的判定與性質、三角函數的定義、等腰三角形的性質、同角的余角相等等知識,證到△AFD∽△BEC是解決本題的關鍵.


科目:初中數學 來源: 題型:解答題
 如圖,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一點(不與點A、B重合),連接CO并延長交⊙O于點D,連接AD.
如圖,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一點(不與點A、B重合),連接CO并延長交⊙O于點D,連接AD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
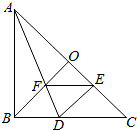 如圖,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折疊,使AB落在AC上,點B與AC上的點E重合,展開后,折痕AD交BO于點F,連接DE、EF,下列結論:①AB=2BD;②圖中有4對全等三角形;③若將△DEF沿EF折疊,則點O不一定落在AC上;④BD=BF,上述結論中正確的是( )
如圖,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折疊,使AB落在AC上,點B與AC上的點E重合,展開后,折痕AD交BO于點F,連接DE、EF,下列結論:①AB=2BD;②圖中有4對全等三角形;③若將△DEF沿EF折疊,則點O不一定落在AC上;④BD=BF,上述結論中正確的是( )| A. | ①②③④ | B. | ②④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
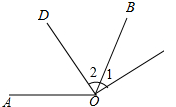 (1)已知一個角是它的余角的一半,求這個角的度數;
(1)已知一個角是它的余角的一半,求這個角的度數;查看答案和解析>>
科目:初中數學 來源: 題型:解答題
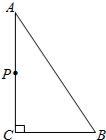 如圖,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若點P從點A出發,以每秒2cm的速度沿折線A-C-B-A運動,設運動時間為t秒(t>0).
如圖,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若點P從點A出發,以每秒2cm的速度沿折線A-C-B-A運動,設運動時間為t秒(t>0).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
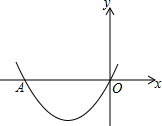 如圖,在直角坐標系xOy中,若拋物線y=$\frac{1}{2}{x^2}$+2x交x軸的負半軸于A,以O為旋轉中心,將線段OA按逆時針方向旋轉α(0°<α≤360°),再沿水平方向向右或向左平移若干個單位長度,對應線段的一個端點正好落在拋物線的頂點處,請直接寫出所有符合題意的α的值是30°或150°.
如圖,在直角坐標系xOy中,若拋物線y=$\frac{1}{2}{x^2}$+2x交x軸的負半軸于A,以O為旋轉中心,將線段OA按逆時針方向旋轉α(0°<α≤360°),再沿水平方向向右或向左平移若干個單位長度,對應線段的一個端點正好落在拋物線的頂點處,請直接寫出所有符合題意的α的值是30°或150°.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
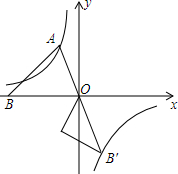 如圖,已知第二象限的點A在反比例函數y=-$\frac{\sqrt{3}}{x}$上,過點A作AB⊥AO交x軸于點B,∠AOB=60°.將△AOB繞點O逆時針旋轉120°,點B的對應點B′恰好落在反比例函數y=$\frac{k}{x}$上,則k的值為( )
如圖,已知第二象限的點A在反比例函數y=-$\frac{\sqrt{3}}{x}$上,過點A作AB⊥AO交x軸于點B,∠AOB=60°.將△AOB繞點O逆時針旋轉120°,點B的對應點B′恰好落在反比例函數y=$\frac{k}{x}$上,則k的值為( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -4$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com