
 如圖,點B、C、D都在半徑為12的⊙O上,過點C作AC∥BD交OB的延長線于點A,連接CD,已知∠CDB=∠OBD=30°.
如圖,點B、C、D都在半徑為12的⊙O上,過點C作AC∥BD交OB的延長線于點A,連接CD,已知∠CDB=∠OBD=30°.分析 (1)首先證明四邊形ABDC為平行四邊形,推出∠A=∠D=30°,∵∠AOC=2∠D=60°,由此可以證明∠ACO=90°即可.
(2)在直角△BEO中,∠OBD=30°,OB=12,推出OE=$\frac{1}{2}$OB=6,BE=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,根據BD=2BE=12$\sqrt{3}$,即可即可解決問題.
(3)易證△OEB≌△CED,推出S陰影=S扇形BOC,由此即可計算.
解答 (1)證明:連接OC,OC交BD于E,
∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∵∠CDB=∠OBD,
∴CD∥AB,
又∵AC∥BD,
∴四邊形ABDC為平行四邊形,
∴∠A=∠D=30°,
∴∠OCA=180°-∠A-∠COB=90°,即OC⊥AC
又∵OC是⊙O的半徑,
∴AC是⊙O的切線;
(2)解:由(1)知,OC⊥AC.
∵AC∥BD,
∴OC⊥BD,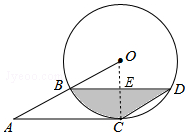
∴BE=DE,
∵在直角△BEO中,∠OBD=30°,OB=12,
∴OE=$\frac{1}{2}$OB=6,BE=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
∴BD=2BE=12$\sqrt{3}$;
(3)解:在△OEB和△CED中,
$\left\{\begin{array}{l}{OE=EC}\\{∠OEB=∠CED}\\{BE=DE}\end{array}\right.$,
∴△OEB≌△CED,
∴S陰影=S扇形BOC
∴S陰影=$\frac{60π•1{2}^{2}}{360}$=24π.
答:陰影部分的面積是24π.
點評 本題考查切線的判定、垂徑定理、扇形的面積公式,全等三角形的判定和性質.平行四邊形的判定和性質等知識,解題的關鍵是發現四邊形ABDC是平行四邊形,屬于中考常考題型.


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | -6、1 | B. | 6、1 | C. | 6、-1 | D. | -6、-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
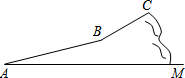 今年“五一”假期,某數學活動小組組織一次登山活動.他們從山腳下A點出發沿斜坡AB到達B點,再從B點沿斜坡BC到達山頂C點,路線如圖所示.斜坡AB的長為1040米,斜坡BC的長為400米,在C點測得B點的俯角為30°,.已知A點海拔191米,C點海拔791米.
今年“五一”假期,某數學活動小組組織一次登山活動.他們從山腳下A點出發沿斜坡AB到達B點,再從B點沿斜坡BC到達山頂C點,路線如圖所示.斜坡AB的長為1040米,斜坡BC的長為400米,在C點測得B點的俯角為30°,.已知A點海拔191米,C點海拔791米.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com