
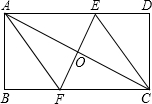
 如圖,已知四邊形ABCD是矩形,對角線AC的垂直平分線交AD于點E,交BC于點F,連接AF,CE,解答下列問題:
如圖,已知四邊形ABCD是矩形,對角線AC的垂直平分線交AD于點E,交BC于點F,連接AF,CE,解答下列問題:分析 (1)由ASA證明△AOE≌△COF,得出對應邊相等EO=FO,證出四邊形AFCE為平行四邊形,再由FE⊥AC,即可得出結論.
(2)由勾股定理和根與系數的關系得出方程,解方程求出m=1或m=-5,再由根的判別式即可得出m的值.
解答 (1)證明:∵四邊形ABCD是矩形,
∴AE∥FC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
在△AOE和△COF中,$\left\{\begin{array}{l}{∠EAO=∠FCO}&{\;}\\{AO=CO}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴EO=FO,
∴四邊形AFCE為平行四邊形,
又∵FE⊥AC,
∴平行四邊形AECF為菱形.
(2)解:在△ABF中,∵∠ABF=90°,
∴AB2+BF2=AF2,
∴AF2=a2+b2=(a+b)2-2ab,
由根與系數的關系得:a+b=2(m+1),ab=m2+1,
∴AF2=[2(m+1)]2-2(m2+1)=2m2+8m+2,
∵菱形AECF的周長為8$\sqrt{3}$,
∴AF=2$\sqrt{3}$,
∴2m2+8m+2=(2$\sqrt{3}$)2,
解得:m=1或m=-5,
∵原方程有實數根,則△≥0,
∴[-2(m+1)]2-4(m2+1)≥0,
∴m=-5不合題意,舍去,
∴m=1,
即當m=1時,菱形AECF的周長為8$\sqrt{3}$.
點評 本題考查了矩形的性質、菱形的判定方法、平行四邊形的判定方法、全等三角形的判定與性質、勾股定理、根與系數的關系以及根的判別式;熟練掌握矩形的性質,證明三角形全等是解決問題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 5 | C. | 1或5 | D. | 無法計算 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
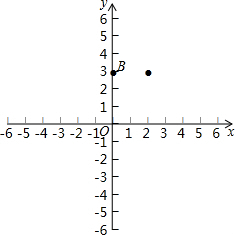 已知拋物線y=ax2+bx+c的頂點為A,經過點B(0,3)和點(2,3),與x軸交于C,D兩點,(點C在點D的左側),且OD=OB.
已知拋物線y=ax2+bx+c的頂點為A,經過點B(0,3)和點(2,3),與x軸交于C,D兩點,(點C在點D的左側),且OD=OB.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
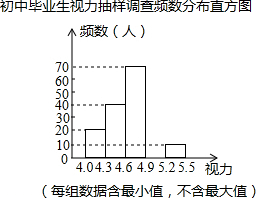 某區對即將參加中考的5000名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和不完整的頻數分布直方圖,請根據圖表信息回答下列問題:
某區對即將參加中考的5000名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和不完整的頻數分布直方圖,請根據圖表信息回答下列問題:| 視力 | 頻數(人) | 頻率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com