
分析 (1)分8≤x≤14和14<x≤30兩種情況,根據“總利潤=單件利潤×銷售量”可得函數解析式;
(2)就(1)中所列函數解析式,配方成頂點式根據二次函數的性質求得函數的最值即可.
解答 解:(1)當8≤x≤14時,每天能銷售該商品[100+10(14-x)]件,y=(x-8)[100+10(14-x)]=-10x2+320x-1920;
當14<x≤30時,每天能銷售該商品[100-4(x-14)]件,y=(x-8)[100-4(x-14)]=-4x2+188x-1248;
(2)當8≤x≤14時,y=-10x2+320x-1920=-10(x-16)2+640,
∵-10<0,
∴拋物線開口向下,當x<16時y隨x的增大而增大,
又8≤x≤14,
∴當x=14時,y最大=-10×(14-16)2+640=600(元);
當14<x≤30時,y=-4x2+188x-1248=-4(x-23.5)2+961,
∵-4<0,
∴拋物線開口向下,
又14<x≤30且x是整數,
所以當x=23或x=24時,y最大=-4(23-23.5)2+961=960(元);
由于600<960,
所以當每件商品的售價為23元或24元時,該超市每天銷售該商品的利潤最大,最大利潤是960元.
點評 本題主要考查二次函數的應用,理解題意分類討論,并依據相等關系列出函數解析式,熟練掌握二次函數的性質是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| x | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 |
| ax2+bx+c | -2 | -$\frac{1}{4}$ | 1 | $\frac{7}{4}$ | 2 | $\frac{7}{4}$ | 1 | -$\frac{1}{4}$ | -2 |
| A. | -$\frac{1}{2}$<x1<0,$\frac{3}{2}$<x2<2 | B. | -1<x1<-$\frac{1}{2}$,2<x2<$\frac{5}{2}$ | ||
| C. | -$\frac{1}{2}$<x1<0,2<x2<$\frac{5}{2}$ | D. | -1<x1<-$\frac{1}{2}$,$\frac{3}{2}$<x2<2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知∠A=∠F,AB∥EF,BC=DE,請說明AD∥CF.
如圖,已知∠A=∠F,AB∥EF,BC=DE,請說明AD∥CF.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
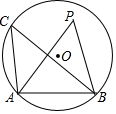 如圖,AB是⊙O的弦,點C在⊙O上,∠ACB=40°,點P在⊙O的內部,且點C、點P在AB同側,則∠APB的角度是( )
如圖,AB是⊙O的弦,點C在⊙O上,∠ACB=40°,點P在⊙O的內部,且點C、點P在AB同側,則∠APB的角度是( )| A. | 大于40° | B. | 等于40° | C. | 小于40° | D. | 無法確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
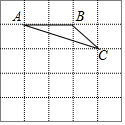 在如圖所示的方格中,每個小正方形的邊長為1,點A、B、C在方格紙中小正方形的頂點上.
在如圖所示的方格中,每個小正方形的邊長為1,點A、B、C在方格紙中小正方形的頂點上.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
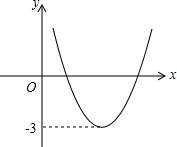 如圖,已知函數y=ax2+bx+c的圖象如圖所示,那么關于x的方程ax2+bx+c+2=0的根的情況是( )
如圖,已知函數y=ax2+bx+c的圖象如圖所示,那么關于x的方程ax2+bx+c+2=0的根的情況是( )| A. | 有兩個同號不相等的實數根 | B. | 有兩個異號實數根 | ||
| C. | 有兩個相等實數根 | D. | 無實數根 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com