
 如圖,在△ABC中,已知點D、E、F分別為邊BC、AD、CE的中點,且△ABC的面積是4cm2,則陰影部分面積等于( )
如圖,在△ABC中,已知點D、E、F分別為邊BC、AD、CE的中點,且△ABC的面積是4cm2,則陰影部分面積等于( )| A. | 2cm2 | B. | 1cm2 | C. | $\frac{1}{4}$cm2 | D. | $\frac{1}{2}$cm2 |
分析 因為點F是CE的中點,所以△BEF的底是△BEC的底的一半,△BEF高等于△BEC的高;同理,D、E、分別是BC、AD的中點,△EBC與△ABC同底,△EBC的高是△ABC高的一半;利用三角形的等積變換可解答.
解答  解:如圖,點F是CE的中點,
解:如圖,點F是CE的中點,
∴△BEF的底是EF,△BEC的底是EC,即EF=$\frac{1}{2}$EC,而高相等,
∴S△BEF=$\frac{1}{2}$S△BEC,
同理得,S△EBC=$\frac{1}{2}$S△ABC,
∴S△BEF=$\frac{1}{4}$S△ABC,且S△ABC=4,
∴S△BEF=1,
即陰影部分的面積為1.
故選B.
點評 本題主要考查了三角形面積的等積變換:若兩個三角形的高(或底)相等,其中一個三角形的底(或高)是另一個三角形的幾倍,那么這個三角形的面積也是另一個三角形面積的幾倍.


科目:初中數學 來源: 題型:選擇題
| A. | 沒有交點 | |
| B. | 只有一個交點,在x軸的負半軸上 | |
| C. | 有兩個交點,都在x軸的正半軸 | |
| D. | 有兩個交點,分別在x軸的正、負半軸上 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x=3 | B. | x=-2 | C. | x=2 | D. | x=0 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ①② | B. | ①③ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 10(1-x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1+x)2=16.9 | D. | 16.9(1+x)2=10 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
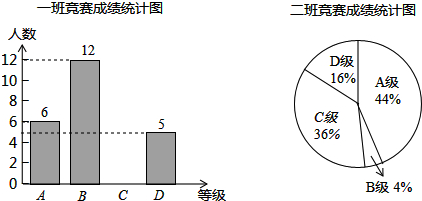
| 平均數(分) | 中位數(分) | 眾數(分) | 方差 | |
| 一班 | a | b | 90 | 106.24 |
| 二班 | 87.6 | 80 | c | 138.24 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com