
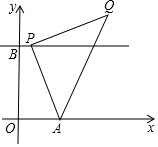
 如圖,在平面直角坐標系中,A(1,0),B(0,2),過點B作直線l∥x軸,點P(a,2)是直線l上的動點,以AP為邊在AP右側作等腰Rt△APQ,使∠APQ=Rt∠.
如圖,在平面直角坐標系中,A(1,0),B(0,2),過點B作直線l∥x軸,點P(a,2)是直線l上的動點,以AP為邊在AP右側作等腰Rt△APQ,使∠APQ=Rt∠.分析 (1)①證明△BQM≌△ABO,得出BM=AO=1,QM=BO=2,求出OM=3,即可得出結果;
②由最短路徑問題求出點A關于y軸的對稱點,由勾股定理求出DQ的長,用待定系數法求出直線DQ的解析式,即可得出點C的坐標;
(2)證明三角形全等同(1),即可得出結果.
解答 解: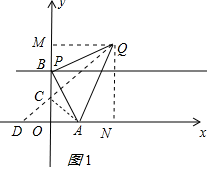 (1)①a=0時,P與B重合,如圖1所示:
(1)①a=0時,P與B重合,如圖1所示:
作QM⊥y軸于M,
∵A(1,0),B(0,2),
∴AO=1,BO=2,
∵△APQ是等腰直角三角形,
∴∠ABQ=90°,BA=BQ,由角的互余關系得:∠ABO=∠BQM,
在△BQM和△ABO中,$\left\{\begin{array}{l}{∠QMB=∠BOA=90°}&{\;}\\{∠BQM=∠ABO}&{\;}\\{BQ=BA}&{\;}\end{array}\right.$,
∴△BQM≌△ABO(AAS),
∴BM=AO=1,QM=BO=2,
∴OM=3,
∴點Q的坐標是(2,3);
故答案為:(2,3);
②作點A關于y軸的對稱點D(-1,0),連接DQ交y軸于C,
此時CA=CD,CA+CQ的值最小,CA+CQ=DQ=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
即CA+CQ的最小值為3$\sqrt{2}$;
設直線DQ的解析式為y=kx+b,
根據題意得:$\left\{\begin{array}{l}{2k+b=3}\\{-k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直線DQ的解析式為y=x+1,
當x=0時,y=1,
∴點C的坐標為(0,1);
故答案為:3$\sqrt{2}$,(0,1);
(2)如圖2所示:作AE⊥BP,QF⊥BP,同(1)①得:△APE≌△PQF,
∴PE=FQ=BP-BE=3-1=2,AE=PF=2,
∴BF=3+2=5,
∴點Q的坐標為(5,0).
點評 本題是三角形綜合題目,考查了全等三角形的判定與性質、勾股定理、最短路徑問題、軸對稱的性質、待定系數法求直線的解析式等知識;本題綜合性強,有一定難度,證明三角形全等是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
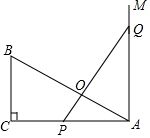 如圖,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射線AM⊥AC,點P在AC上運動(不與點A,C重合),點Q在AM上運動(不與點A重合),且始終保持PQ=AB.
如圖,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射線AM⊥AC,點P在AC上運動(不與點A,C重合),點Q在AM上運動(不與點A重合),且始終保持PQ=AB.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于點E,則下列結論錯誤的是( )
如圖,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于點E,則下列結論錯誤的是( )| A. | BD+ED=BC | B. | ED+AC>AD | C. | DA平分∠EDC | D. | DE平分∠ADB |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
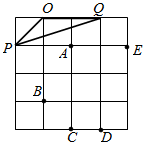 如圖,△OPQ在邊長為1個單位的方格紙中,它們的頂點在小正方形頂點位置,點A,B,C,D,E也是小正方形的頂點,從點A,B,C,D,E中選取三個點所構成的三角形與△OPQ相似,那么這個三角形是△CDB.
如圖,△OPQ在邊長為1個單位的方格紙中,它們的頂點在小正方形頂點位置,點A,B,C,D,E也是小正方形的頂點,從點A,B,C,D,E中選取三個點所構成的三角形與△OPQ相似,那么這個三角形是△CDB.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
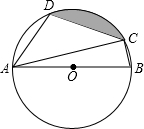 如圖,四邊形ABCD是⊙O的內接四邊形,AB是⊙O的直徑,∠D=108°,連接AC.
如圖,四邊形ABCD是⊙O的內接四邊形,AB是⊙O的直徑,∠D=108°,連接AC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com