
 如圖,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分線.
如圖,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分線.分析 (1)利用基本作圖(作已知角的平分線)作DN平分∠ADC;
(2)根據等腰三角形的性質得∠BAD=∠CAD,再利用AM是△ABC外角∠CAE的平分線可得∠FAD=90°,則可判斷AF∥BC,利用平行線的性質得∠CDF=∠AFD,加上∠AFD=∠ADF,所以∠CDF=∠ADF,然后根據等腰三角形的判定方法可得到△ADF是等腰直角三角形.
解答 解:(1)如圖,DN為所作;
(2)△ADF是等腰直角三角形.
理由如下:∵AB=AC,AD是高,
∴∠BAD=∠CAD,
又∵AM是△ABC外角∠CAE的平分線,
∴∠FAD=$\frac{1}{2}$×180°=90°,
∴AF∥BC,
∴∠CDF=∠AFD,
又∵∠AFD=∠ADF,
∴∠CDF=∠ADF,
∴AD=AF,
∴△ADF是等腰直角三角形.
點評 本題考查了作圖-基本作圖:熟練掌握基本作圖(作一條線段等于已知線段;作一個角等于已知角;作已知線段的垂直平分線;作已知角的角平分線;過一點作已知直線的垂線).也考查了等腰三角形的判斷與性質.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
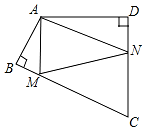 如圖,四邊形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分別找一點M、N,使△AMN周長最小時,則∠AMN+∠ANM的度數為( )
如圖,四邊形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分別找一點M、N,使△AMN周長最小時,則∠AMN+∠ANM的度數為( )| A. | 135° | B. | 130° | C. | 125° | D. | 120° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x≠4 | B. | x≤4 | C. | x<4 | D. | 1<x<4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com