
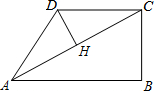
 在四邊形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,點H為垂足,設AB=x,AD=y,則y關于x的函數關系用圖象大致可以表示為( )
在四邊形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,點H為垂足,設AB=x,AD=y,則y關于x的函數關系用圖象大致可以表示為( )| A. | 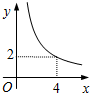 | B. | 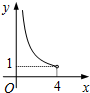 | C. | 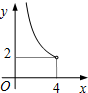 | D. | 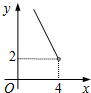 |
分析 先利用線段垂直平分線的性質得到AD=CD=y,AH=CH=$\frac{1}{2}$AC=2,∠CHD=90°,再證明△CDH∽△ACB,則利用相似比可得到y=$\frac{8}{x}$(0<x<4),然后利用反比例函數的圖象和自變量的取值范圍對各選項進行判斷.
解答 解:∵DH垂直平分AC,
∴AD=CD=y,AH=CH=$\frac{1}{2}$AC=2,∠CHD=90°,
∵CD∥AB,
∴∠DCH=∠BAC,
∴△CDH∽△ACB,
∴$\frac{CD}{AC}$=$\frac{CH}{AB}$,$\frac{y}{4}$=$\frac{2}{x}$,
∴y=$\frac{8}{x}$(0<x<4).
故選C.
點評 BE題考查了函數圖象:函數圖象是典型的數形結合,圖象應用信息廣泛,通過看圖獲取信息,不僅可以解決生活中的實際問題,還可以提高分析問題、解決問題的能力.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
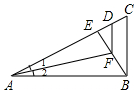 如圖,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,則( )
如圖,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,則( )| A. | ∠1=∠EFD | B. | BE=CE | C. | BF-DE=CD | D. | DF∥BC |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com